0.003 Is 1 10 Of Which Decimal
Arias News
May 12, 2025 · 4 min read
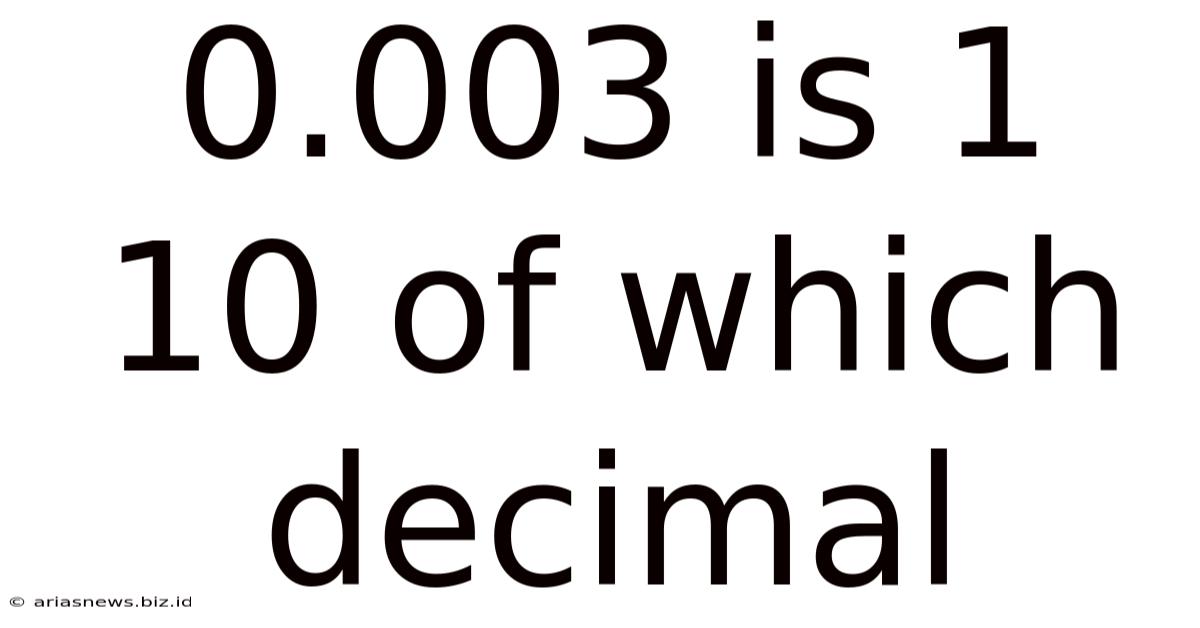
Table of Contents
0.003 is 1/10 of Which Decimal? Unraveling Decimal Relationships
Understanding decimal relationships is crucial for various mathematical applications, from everyday calculations to advanced scientific computations. This article delves into the question: "0.003 is 1/10 of which decimal?" We'll explore the solution, the underlying principles, and practical applications to solidify your understanding of decimals.
Understanding Decimals and Fractions
Before tackling the core problem, let's refresh our understanding of decimals and their relationship with fractions. Decimals are a way of representing fractional numbers using a base-10 system. The decimal point separates the whole number part from the fractional part. Each position to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
For instance, the decimal 0.003 can be expressed as a fraction:
0.003 = 3/1000
This means there are 3 parts out of 1000 equal parts.
Solving the Problem: 0.003 is 1/10 of Which Decimal?
The problem states that 0.003 is one-tenth (1/10) of another decimal. To find this decimal, we need to perform the inverse operation of dividing by 1/10, which is equivalent to multiplying by 10.
Therefore, we multiply 0.003 by 10:
0.003 x 10 = 0.03
Therefore, 0.003 is 1/10 of 0.03.
Let's verify this:
1/10 of 0.03 = 0.03 / 10 = 0.003
The calculation confirms our solution.
Expanding the Concept: Decimal Multipliers and Divisors
This problem highlights a fundamental aspect of decimal arithmetic: multiplying a decimal by 10, 100, 1000, etc., shifts the decimal point to the right by the number of zeros in the multiplier. Conversely, dividing a decimal by these powers of 10 shifts the decimal point to the left.
Here are some examples:
- Multiplying: 0.003 x 100 = 0.3 (decimal point moves two places to the right)
- Multiplying: 0.003 x 1000 = 3 (decimal point moves three places to the right)
- Dividing: 0.03 / 10 = 0.003 (decimal point moves one place to the left)
- Dividing: 0.3 / 100 = 0.003 (decimal point moves two places to the left)
Understanding these rules is critical for efficient decimal calculations. They avoid the need for cumbersome long division or multiplication in many cases.
Real-World Applications of Decimal Relationships
The concepts discussed here aren't just theoretical; they have numerous practical applications:
1. Finance and Accounting:
- Calculating interest: Interest rates are often expressed as decimals (e.g., 0.05 for 5%). Understanding how decimals relate to percentages is vital for calculating interest earned or paid on loans, investments, and savings accounts. Compound interest calculations heavily rely on understanding decimal multiplication and division.
- Currency conversions: Exchange rates are expressed as decimals. Converting currencies requires multiplying or dividing by these decimal exchange rates.
- Tax calculations: Sales tax, income tax, and other taxes are often expressed as decimals or percentages, requiring accurate decimal calculations.
2. Science and Engineering:
- Measurements: Scientific measurements frequently involve decimals, often expressed in metric units (e.g., meters, grams, liters). Converting between units often involves multiplication or division by powers of 10.
- Data analysis: Statistical analysis often relies on decimal calculations to interpret data and draw conclusions.
- Engineering design: Precision engineering requires extremely accurate decimal calculations for dimensions, tolerances, and other parameters.
3. Everyday Life:
- Shopping: Calculating discounts, sales tax, and comparing prices often involves decimal calculations.
- Cooking and baking: Recipes often use decimals to specify ingredient quantities (e.g., 0.5 cups of sugar).
- Travel: Calculating distances, fuel consumption, and travel times frequently involves decimal computations.
Advanced Decimal Concepts: Recurring Decimals and Significant Figures
While this article focused on simple decimal relationships, let's briefly touch upon more advanced concepts:
1. Recurring Decimals:
Some fractions, when converted to decimals, result in recurring (repeating) decimals. For example, 1/3 = 0.3333... Understanding how to represent and manipulate these recurring decimals is crucial for accurate calculations.
2. Significant Figures:
In scientific and engineering applications, it's essential to consider significant figures when working with decimals. Significant figures represent the precision of a measurement. Understanding how to round decimals appropriately is important for avoiding errors in calculations.
Conclusion: Mastering Decimal Relationships for Success
Mastering decimal relationships is a foundational skill applicable to various fields. By understanding the principles of decimal multiplication and division, you can confidently tackle numerous problems in mathematics, science, finance, and everyday life. This article aimed to provide a thorough explanation of the core concept, along with practical applications and a glimpse into more advanced decimal concepts. Continue practicing decimal calculations and exploring related concepts to strengthen your mathematical abilities. Remember that consistent practice and a solid grasp of fundamental principles are key to achieving mastery. Understanding decimal relationships empowers you to navigate the numerical world with confidence and accuracy.
Latest Posts
Latest Posts
-
How To Address A Letter To A Nursing Home Resident
May 12, 2025
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
Related Post
Thank you for visiting our website which covers about 0.003 Is 1 10 Of Which Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.