0.07 Is 10 Times As Great As
Arias News
May 12, 2025 · 5 min read
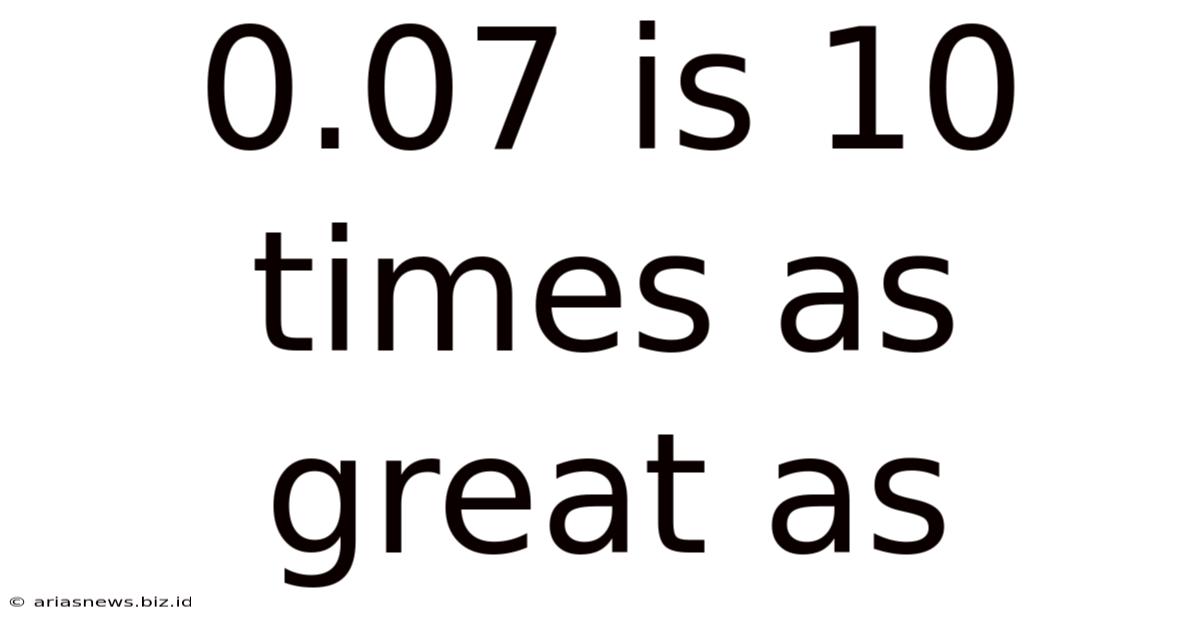
Table of Contents
0.07 is 10 Times as Great as: Understanding Decimal Place Value and Comparisons
This article delves into the mathematical concept behind the statement "0.07 is 10 times as great as," exploring the underlying principles of decimal place value and providing practical examples to solidify understanding. We'll move beyond the simple statement to explore broader implications of decimal comparisons and their application in various fields.
Understanding Decimal Place Value
Before tackling the core statement, it's crucial to grasp the concept of decimal place value. Decimals represent numbers less than one, expressed using a decimal point. Each position to the right of the decimal point represents a progressively smaller fraction of one. The first position after the decimal is the tenths place (1/10 or 0.1), the second is the hundredths place (1/100 or 0.01), the third is the thousandths place (1/1000 or 0.001), and so on.
Key takeaway: Understanding place value is the cornerstone of comparing decimals. Each position represents a power of ten, decreasing from left to right.
Breaking Down "0.07 is 10 Times as Great as"
The statement declares that 0.07 is ten times larger than another number. To find that number, we perform the inverse operation of multiplication: division. We divide 0.07 by 10:
0.07 ÷ 10 = 0.007
Therefore, 0.07 is 10 times as great as 0.007.
This demonstrates the relationship between the two numbers and how a shift in the decimal point affects their magnitude. Moving the decimal point one place to the left divides the number by 10, while moving it one place to the right multiplies the number by 10.
Practical Applications and Real-World Examples
The understanding of decimal comparisons isn't confined to theoretical mathematics. It's a fundamental concept with widespread applications across numerous fields:
1. Finance and Accounting:
- Calculating interest: Understanding decimal place value is critical when calculating compound interest rates. A difference of even a few hundredths of a percentage point can significantly impact the final amount over time.
- Currency conversions: Converting currencies involves working with decimals. Accurate calculations are essential for international trade and finance.
- Stock market analysis: Stock prices are expressed as decimals. Understanding the change in decimal points represents the increase or decrease in stock value.
2. Science and Measurement:
- Metric system: The metric system relies heavily on decimal multiples and submultiples of base units (like meters, liters, and grams). Conversions between units frequently involve moving decimal points.
- Scientific notation: Scientific notation uses powers of 10 to express very large or very small numbers, directly relating to decimal place value. For example, the speed of light is approximately 3 x 10⁸ meters per second.
- Data analysis: Scientific data often involves decimal values that need to be compared and analyzed to draw conclusions.
3. Engineering and Technology:
- Precision engineering: Engineering drawings and specifications often involve precise measurements expressed in decimals. Even small variations in decimal places can have significant impacts on the functionality of a part or system.
- Computer programming: Decimal numbers are fundamental in computer programming, used in calculations, data representation, and algorithmic operations.
- Digital signal processing: Many signals are represented digitally using decimals. Understanding the relationship between these decimal values is crucial in analyzing and processing the signals.
Expanding the Concept: Comparing Larger Decimals
Let's extend the concept beyond 0.07 and 0.007. Consider the following scenarios:
- 2.5 is 10 times as great as 0.25: Dividing 2.5 by 10 results in 0.25.
- 10.0 is 10 times as great as 1.0: Dividing 10.0 by 10 results in 1.0
- 0.0005 is 10 times as great as 0.00005: Dividing 0.0005 by 10 results in 0.00005
These examples consistently demonstrate the principle: Dividing a decimal by 10 results in a number that is one-tenth the original value, effectively shifting the decimal point one place to the left. Conversely, multiplying a decimal by 10 shifts the decimal point one place to the right.
Advanced Comparisons and Problem-Solving
The core principle of decimal comparison can be applied to more complex problems. Consider a scenario where you need to determine if 0.07 is greater than, less than, or equal to another decimal, such as 0.7. By examining the place value of each digit, we can determine that 0.7 (seven-tenths) is considerably larger than 0.07 (seven-hundredths).
Another example involves comparing decimals with varying numbers of decimal places. To compare 0.125 and 0.12, we can add a trailing zero to 0.12, making it 0.120. This allows for a straightforward comparison, revealing that 0.125 is greater than 0.12.
Avoiding Common Mistakes
Common mistakes when dealing with decimal comparisons stem from misunderstandings of place value. These errors are usually related to:
- Ignoring leading zeros: Leading zeros to the left of a non-zero digit do not affect the value of the number (0.07 is equal to 0.0700). However, they are crucial for placing the digits in their correct positions within the place value system.
- Misplacing the decimal point: Incorrect placement of the decimal point dramatically alters the numerical value. Always carefully check the position of the decimal point during calculations and comparisons.
- Incorrect rounding: Rounding numbers inappropriately can introduce errors into comparisons. It is essential to only round numbers according to the level of precision required.
Mastering Decimal Comparisons: Practice Makes Perfect
The ability to confidently compare decimals is essential for success in many fields. Consistent practice with various examples and problem-solving is crucial to mastering this skill. Work through several examples, applying the techniques and principles discussed above. Engage in problems that require comparisons of decimals with different numbers of decimal places. By doing so, you will build a solid foundation of understanding and confidence in tackling decimal comparison problems.
Conclusion: The Importance of Precision
The seemingly simple statement, "0.07 is 10 times as great as," underscores a fundamental principle in mathematics: the significance of decimal place value. Understanding decimal comparisons is not just a mathematical exercise; it is a crucial skill with practical implications in a wide range of fields, from finance and science to engineering and technology. By mastering decimal comparisons, we enhance our ability to analyze data, make accurate calculations, and navigate a world increasingly reliant on precise numerical representations. The accuracy of our understanding and application of this concept directly impacts the validity and reliability of results in countless endeavors. Continual practice and a deep understanding of place value will ensure proficiency in handling these crucial mathematical operations.
Latest Posts
Latest Posts
-
Can Rose Of Sharon Roots Damage Foundation
May 12, 2025
-
How Do You Say 12 30 In Spanish
May 12, 2025
-
Closeness Of A Measurement To The True Value
May 12, 2025
-
What Foods Do They Eat In Australia For Christmas
May 12, 2025
-
Can You Reheat Food With Sour Cream In It
May 12, 2025
Related Post
Thank you for visiting our website which covers about 0.07 Is 10 Times As Great As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.