0.6 Divided By 10 To The Power Of 2
Arias News
May 10, 2025 · 5 min read
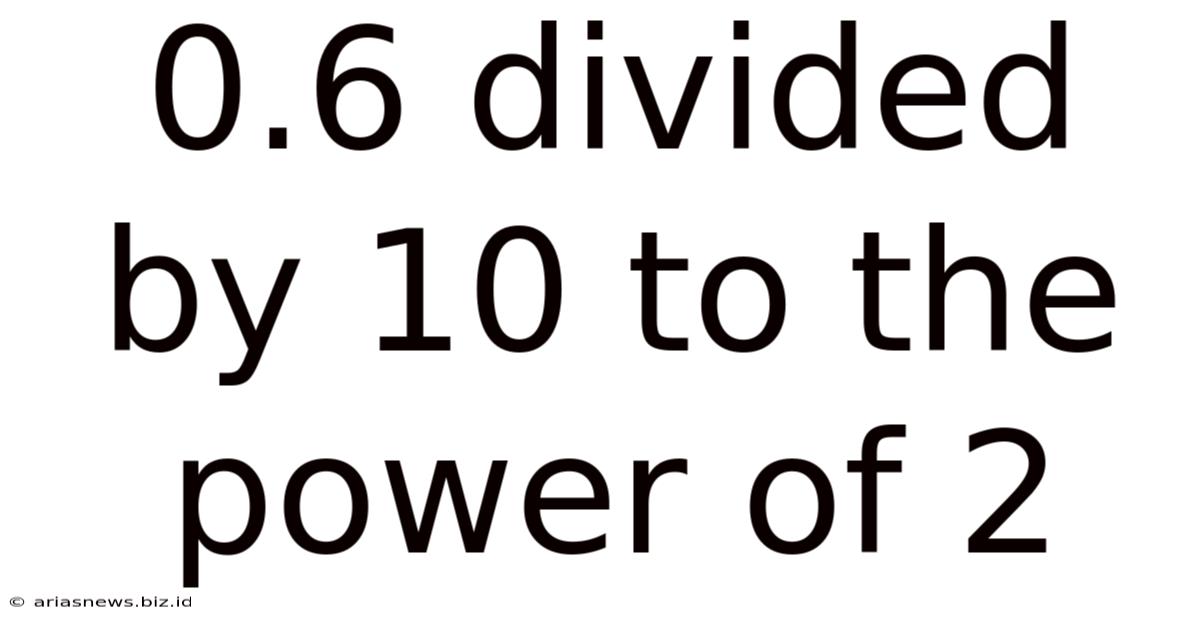
Table of Contents
Decoding 0.6 Divided by 10 to the Power of 2: A Deep Dive into Exponents and Decimal Division
This seemingly simple mathematical problem, 0.6 divided by 10², hides a wealth of underlying concepts crucial to understanding mathematics, particularly exponents and decimal division. This article will dissect this problem, exploring the fundamental principles involved, offering multiple approaches to solving it, and extending the discussion to encompass broader applications in various fields.
Understanding the Components: Exponents and Decimal Numbers
Before tackling the problem directly, let's refresh our understanding of the core components: exponents and decimal numbers.
Exponents (or Indices): An exponent indicates how many times a number (the base) is multiplied by itself. In the expression 10², the base is 10 and the exponent is 2. This means 10² = 10 x 10 = 100. Exponents are fundamental in various areas, from scientific notation (representing extremely large or small numbers) to calculating compound interest and modeling exponential growth or decay.
Decimal Numbers: Decimal numbers are numbers that contain a decimal point, separating the whole number part from the fractional part. 0.6 represents six-tenths, or 6/10. Understanding decimal place value is crucial for operations like division and multiplication. Each place to the right of the decimal point represents a decreasing power of 10: tenths (10⁻¹), hundredths (10⁻²), thousandths (10⁻³), and so on.
Method 1: Solving 0.6 ÷ 10² Directly
The most straightforward approach is to calculate 10² first and then perform the division:
-
Calculate 10²: 10² = 10 x 10 = 100
-
Perform the division: 0.6 ÷ 100 = 0.006
Therefore, 0.6 divided by 10² equals 0.006.
This method highlights the direct application of exponent rules and decimal division. It's a clear and concise approach suitable for basic calculations.
Method 2: Using Scientific Notation
Scientific notation provides an elegant way to handle both large and small numbers. It expresses a number as a product of a number between 1 and 10 and a power of 10. Let's express 0.6 in scientific notation:
0.6 = 6 x 10⁻¹
Now, let's substitute this into our problem:
(6 x 10⁻¹) ÷ 10²
Using the rules of exponents (when dividing powers with the same base, subtract the exponents):
6 x 10⁻¹⁻² = 6 x 10⁻³ = 0.006
This method showcases the power of scientific notation in simplifying calculations, especially when dealing with very large or very small numbers. The manipulation of exponents becomes more intuitive in this format.
Method 3: Understanding Decimal Shifting
Dividing a decimal number by powers of 10 involves shifting the decimal point. Dividing by 10 moves the decimal point one place to the left. Dividing by 100 (10²) moves the decimal point two places to the left. Dividing by 1000 (10³) moves it three places to the left, and so on.
In our problem, 0.6 ÷ 10² means we shift the decimal point in 0.6 two places to the left:
0.6 becomes 0.006
This method offers a quick visual approach, particularly useful for mental calculations or estimations. It emphasizes the direct relationship between decimal place value and powers of 10.
Extending the Concept: Applications in Real-World Scenarios
The principles demonstrated in solving 0.6 ÷ 10² extend far beyond simple arithmetic. Here are a few examples:
-
Scientific Measurements: In science, measurements often involve extremely small or large numbers. Scientific notation, directly related to the concept of exponents, is essential for representing these values concisely and accurately. For instance, the size of an atom or the distance between stars is often expressed using scientific notation. Dividing these values by powers of 10 is frequently required in calculations.
-
Financial Calculations: Compound interest, a crucial concept in finance, utilizes exponential growth. Understanding how to manipulate exponents is essential for accurately calculating interest earned or owed over time. Dividing interest rates or principal amounts by powers of 10 is common in various financial models.
-
Computer Science: Binary numbers, the foundation of computer systems, are based on powers of 2. Understanding exponents is fundamental to comprehending data storage, memory allocation, and various computational processes. Dividing binary values by powers of 2 is a common operation in programming and computer architecture.
-
Engineering and Physics: Many engineering and physics principles rely on exponential relationships, such as radioactive decay, the intensity of light, and the behavior of electrical circuits. These calculations frequently involve manipulating exponents and dividing quantities by powers of 10.
Beyond the Basics: Exploring Further Mathematical Concepts
This seemingly simple problem opens doors to exploring more advanced mathematical concepts:
-
Logarithms: Logarithms are the inverse of exponents. Understanding logarithms allows us to solve equations involving exponents more easily. For example, if we had to solve for x in the equation 10ˣ = 0.006, logarithms would be the key.
-
Calculus: Exponential and logarithmic functions play a central role in calculus, which deals with rates of change. Understanding exponents is a prerequisite for tackling derivatives and integrals involving these functions.
-
Linear Algebra: Matrices and vectors, fundamental to linear algebra, frequently involve exponential terms and powers. The principles of exponent manipulation are essential for computations in linear algebra.
Conclusion: The Significance of Understanding Exponents and Decimal Division
Solving 0.6 divided by 10² may seem trivial at first glance, but its underlying principles extend far beyond a single calculation. Mastering exponents and decimal division is crucial for success in various fields, from basic arithmetic to advanced scientific and engineering applications. The different methods presented – direct calculation, scientific notation, and decimal shifting – illustrate the versatility and adaptability of mathematical concepts. Understanding these methods not only provides practical skills for problem-solving but also cultivates a deeper appreciation for the interconnectedness of mathematical ideas. The ability to apply these fundamental concepts opens up exciting possibilities for exploring more complex mathematical landscapes. By solidifying your understanding of these core principles, you pave the way for tackling more intricate mathematical challenges and enhancing your problem-solving abilities across numerous disciplines.
Latest Posts
Latest Posts
-
16 Oz Block Of Cheese How Much Shredded
May 10, 2025
-
What Is The Completely Factored Form Of 8x2 50
May 10, 2025
-
What Is The Prime Factorization Of 270
May 10, 2025
-
Saquen Una Hoja De Papel In English
May 10, 2025
-
1 2 Ounce Is Equal To How Many Teaspoons
May 10, 2025
Related Post
Thank you for visiting our website which covers about 0.6 Divided By 10 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.