1 1 2 4 3 9 4
Arias News
Mar 31, 2025 · 5 min read
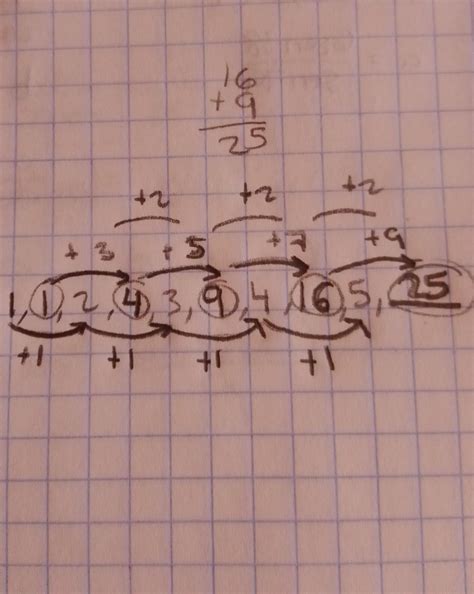
Table of Contents
Unraveling the Sequence: 1 1 2 4 3 9 4 16... and the Beauty of Mathematical Patterns
The seemingly simple sequence, 1 1 2 4 3 9 4 16, initially presents itself as a cryptic puzzle. However, beneath its unassuming façade lies a rich tapestry of mathematical concepts, revealing the underlying elegance and predictability of numerical patterns. This article delves deep into the sequence, exploring its structure, generating functions, and connections to broader mathematical principles. We'll unpack its intricacies and show you how to not only understand it but also predict its continuation and even create similar sequences.
Understanding the Pattern: The Square of the Sequence
The key to unlocking this sequence lies in recognizing the relationship between consecutive pairs of numbers. Notice that the second number in each pair is the square of the first number:
- 1 1² = 1
- 2 2² = 4
- 3 3² = 9
- 4 4² = 16
This simple yet elegant pattern is the foundation of the sequence. Therefore, the sequence can be expressed more formally as pairs of (n, n²), where 'n' represents a natural number. This allows for straightforward continuation: the next numbers in the sequence would be 5, 25; 6, 36; and so on.
Extending the Sequence: Predicting Future Numbers
Applying this understanding, we can easily extend the sequence indefinitely. Following the pattern of (n, n²), the next few terms would be:
- 5, 25
- 6, 36
- 7, 49
- 8, 64
- 9, 81
- 10, 100
And so on. This predictability highlights the power of identifying underlying mathematical relationships. Once the pattern is understood, generating future terms becomes a trivial task.
Generating Functions: A Formal Approach
The sequence can be described more formally using the concept of generating functions. While this approach might seem more complex initially, it offers a powerful tool for analyzing and manipulating sequences. A generating function is a formal power series whose coefficients correspond to the terms of the sequence. In this case, while a single generating function that perfectly captures the interleaved nature of the sequence is complex, we can approach it by considering two separate generating functions: one for the first numbers in each pair (1, 2, 3, 4...) and another for the second numbers in each pair (1, 4, 9, 16...).
The generating function for the first numbers (1, 2, 3, 4...) is simply:
∑_{n=1}^{∞} nx^{n-1} = 1/(1-x)²
This is a well-known generating function for the sequence of natural numbers. For the second sequence (1, 4, 9, 16...), representing the squares, the generating function is slightly more intricate but still derivable using standard techniques in generating functions.
The combined generating function would require a more sophisticated approach, likely involving manipulations of the individual generating functions to accurately represent the alternating nature of the pairs.
Recursive Relationships and Iterative Functions
Another perspective on this sequence involves exploring potential recursive relationships. A recursive relationship defines a term in a sequence based on preceding terms. While a simple, direct recursive relationship might not be immediately apparent, we could define a function that generates pairs:
Let's say we have a function F(n) that generates the nth pair. Then:
F(n) = (n, n²)
This function directly generates the sequence without relying on previous terms, except for the implicit dependence on the input 'n'.
Connections to Other Mathematical Concepts
This seemingly simple sequence touches upon various broader mathematical concepts. It's a direct demonstration of:
- Sequences and Series: The sequence itself is a fundamental example of a numerical sequence.
- Quadratic Functions: The relationship between paired numbers directly represents a quadratic function (f(x) = x²).
- Generating Functions: As discussed earlier, generating functions provide a formal framework for representing and analyzing the sequence.
- Number Theory: The sequence touches upon fundamental properties of numbers and their relationships.
Applications and Further Explorations
Understanding this seemingly simple sequence can open doors to more complex mathematical explorations. The principles applied here extend to more intricate sequences and series. This kind of analysis is crucial in areas like:
- Computer Science: Algorithm design and analysis often involve sequences and series, especially in areas like complexity analysis.
- Physics: Many physical phenomena can be modeled using sequences and series.
- Engineering: Signal processing and control systems frequently use sequences and series.
- Financial Modeling: Financial models often rely on sequences to forecast future trends and values.
Creating Similar Sequences: Exploring Variations
The fundamental principle behind this sequence – pairing a number with its square – allows for the creation of similar sequences. We can generate variations by modifying the operation applied to the first number:
- Cubing: Instead of squaring, we could cube each number: (1, 1), (2, 8), (3, 27), (4, 64)...
- Higher Powers: We can raise the first number to any power: (1, 1^n), (2, 2^n), (3, 3^n)... where 'n' is any positive integer.
- Other Functions: We can use other mathematical functions besides power functions. For example, we could use the factorial function: (1, 1!), (2, 2!), (3, 3!), (4, 4!)...
These variations demonstrate the flexibility and extensibility of the underlying concept.
Conclusion: The Enduring Appeal of Mathematical Patterns
The sequence 1 1 2 4 3 9 4 16 may appear initially mundane. However, through careful analysis, we've uncovered a wealth of mathematical principles and connections. The ability to recognize patterns, understand underlying relationships, and express them formally is a cornerstone of mathematical thinking. This sequence serves as a microcosm of the elegance and power of mathematics, reminding us that even the simplest patterns can reveal deep and fascinating insights. The ability to extrapolate from a simple sequence, predict future values, and explore variations demonstrates the practical applications of mathematical thinking across diverse fields. The journey from a seemingly simple sequence to a deep exploration of generating functions, recursive relationships, and their connections to wider mathematical concepts underscores the enduring appeal of mathematical patterns and their importance in various fields of study and application.
Latest Posts
Latest Posts
-
Who Played Baby Leander In Perry Mason
Apr 02, 2025
-
How Many Eighths Are Equivalent To 1 4
Apr 02, 2025
-
How Long Does It Take To Walk 5 Mile
Apr 02, 2025
-
How Long Is Miracle Whip Good After Opened
Apr 02, 2025
-
How Many Centimeters Is A Paper Clip
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 1 1 2 4 3 9 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
