1/4 Cup + 1/4 Cup Equals How Many Cups
Arias News
Apr 22, 2025 · 5 min read
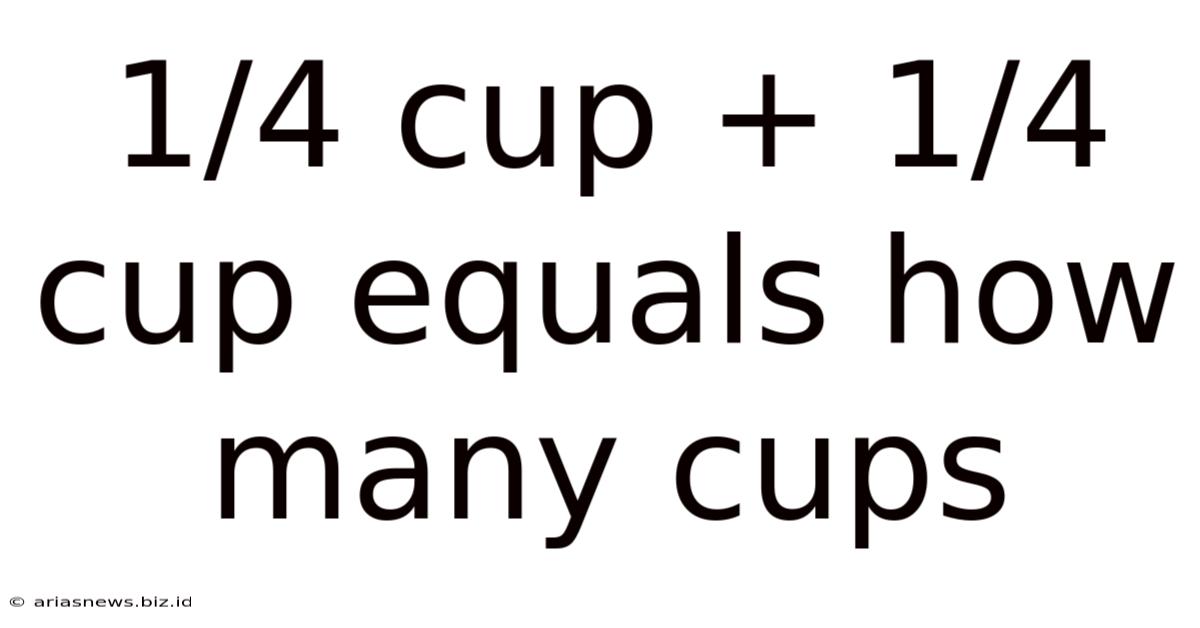
Table of Contents
- 1/4 Cup + 1/4 Cup Equals How Many Cups
- Table of Contents
- 1/4 Cup + 1/4 Cup Equals How Many Cups: A Comprehensive Guide to Fraction Addition
- Understanding Fractions: The Building Blocks
- Adding Fractions with the Same Denominator
- Simplifying Fractions: Reducing to the Lowest Terms
- The Final Answer: 1/4 Cup + 1/4 Cup = 1/2 Cup
- Practical Applications: Beyond the Classroom
- Cooking and Baking: Precision in the Kitchen
- Measurement and Construction: Accuracy in Building
- Sewing and Tailoring: Precision in Fabric Cutting
- Science and Engineering: Precise Calculations
- Finance and Budgeting: Managing Finances
- Expanding Your Knowledge: Adding Fractions with Different Denominators
- Mastering Fractions: A Pathway to Mathematical Proficiency
- Conclusion: The Importance of Precision and Understanding
- Latest Posts
- Latest Posts
- Related Post
1/4 Cup + 1/4 Cup Equals How Many Cups: A Comprehensive Guide to Fraction Addition
This seemingly simple question, "1/4 cup + 1/4 cup equals how many cups?", holds a surprising depth when we explore the underlying mathematical concepts and practical applications. While the answer itself is straightforward, understanding the process allows us to tackle more complex fraction problems confidently. This comprehensive guide will not only provide the answer but also delve into the "why" behind the calculation, offering valuable insights for various applications, from baking and cooking to general math proficiency.
Understanding Fractions: The Building Blocks
Before tackling the addition problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, showing the total number of equal parts the whole is divided into.
In our case, 1/4 represents one part out of four equal parts. Visualize a pie cut into four equal slices. 1/4 represents a single slice.
Adding Fractions with the Same Denominator
Adding fractions with the same denominator is relatively simple. We only need to add the numerators while keeping the denominator unchanged. This is because we're dealing with parts of the same whole.
The Rule: a/c + b/c = (a+b)/c
Let's apply this rule to our problem: 1/4 + 1/4
- Add the numerators: 1 + 1 = 2
- Keep the denominator the same: The denominator remains 4.
- Result: 2/4
Simplifying Fractions: Reducing to the Lowest Terms
The fraction 2/4 represents two parts out of four. We can simplify this fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 2 and 4 is 2. Dividing both the numerator and the denominator by the GCD gives us the simplest form of the fraction.
2 ÷ 2 = 1 4 ÷ 2 = 2
Therefore, 2/4 simplifies to 1/2.
The Final Answer: 1/4 Cup + 1/4 Cup = 1/2 Cup
So, to answer the initial question directly: 1/4 cup + 1/4 cup equals 1/2 cup.
Practical Applications: Beyond the Classroom
Understanding fraction addition isn't just an academic exercise; it has numerous real-world applications, particularly in:
Cooking and Baking: Precision in the Kitchen
Recipes often require precise measurements. Adding fractions of cups or tablespoons is essential for achieving the desired consistency and taste. Incorrectly adding fractions can significantly alter the final product. For example, a recipe calling for 1/4 cup of butter plus 1/4 cup of sugar requires a total of 1/2 cup of the combined ingredients. This knowledge ensures accurate measurements and consistent results.
Measurement and Construction: Accuracy in Building
Many construction projects involve precise measurements and calculations using fractions. Whether it's cutting lumber, mixing concrete, or measuring distances, accurate fraction addition is vital for ensuring the project’s structural integrity and the overall quality of the work. Incorrect calculations can lead to structural weaknesses or misalignments.
Sewing and Tailoring: Precision in Fabric Cutting
In sewing and tailoring, precise measurements are crucial. Patterns often require adding fractional inches to adjust for seam allowances or fit. Accurate fraction addition ensures the garment fits correctly and avoids fabric waste. Mistakes in calculations can result in ill-fitting clothes or unusable fabric.
Science and Engineering: Precise Calculations
In scientific and engineering fields, precise calculations are paramount. Many experiments and designs require careful measurements and the addition of fractional units. Accurate fraction addition ensures accurate data analysis, precise manufacturing, and the overall success of research and development efforts. Errors in calculations can lead to incorrect results or flawed designs.
Finance and Budgeting: Managing Finances
Understanding fractions is important for managing personal finances and understanding financial data. Budgeting often involves allocating portions of income to different expenses. These allocations can be represented as fractions, and accurate addition of these fractions is crucial for tracking expenses and making sound financial decisions. Miscalculations can lead to budgeting problems.
Expanding Your Knowledge: Adding Fractions with Different Denominators
While the initial problem focused on fractions with the same denominator, let's briefly explore adding fractions with different denominators. This requires finding a common denominator—a number that is a multiple of both denominators.
Example: 1/2 + 1/3
- Find the least common multiple (LCM) of the denominators: The LCM of 2 and 3 is 6.
- Convert the fractions to equivalent fractions with the common denominator:
- 1/2 = 3/6 (multiply both numerator and denominator by 3)
- 1/3 = 2/6 (multiply both numerator and denominator by 2)
- Add the numerators: 3/6 + 2/6 = 5/6
The result, 5/6, cannot be simplified further.
Mastering Fractions: A Pathway to Mathematical Proficiency
Mastering fractions is a fundamental step towards achieving mathematical proficiency. From simple addition to complex calculus, a solid understanding of fractions forms the groundwork for more advanced mathematical concepts. It's a skill that transcends academic boundaries and applies to numerous real-world scenarios.
Conclusion: The Importance of Precision and Understanding
The seemingly simple question of 1/4 cup + 1/4 cup highlights the importance of precision and a thorough understanding of basic mathematical concepts. The answer, 1/2 cup, is straightforward, but the process involved emphasizes the practical applications of fraction addition in various aspects of daily life. From cooking to construction, finance to science, the ability to add fractions accurately ensures precision, efficiency, and success in a wide range of endeavors. By solidifying this fundamental understanding, we pave the way for tackling more complex mathematical challenges with confidence and competence. The ability to accurately add fractions is not merely a mathematical skill; it’s a valuable life skill that empowers us to navigate the world with greater precision and understanding.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 90 And 135
May 11, 2025
-
Can A Triangle Be Acute And Scalene
May 11, 2025
-
Can You Get Married If You Have A Warrant
May 11, 2025
-
Enter The Ions Present In A Solution Of K2co3
May 11, 2025
-
85 Cm Is Equal To How Many Inches
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Cup + 1/4 Cup Equals How Many Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.