1/4 Cup + 1/4 Cup Equals What
Arias News
May 09, 2025 · 5 min read
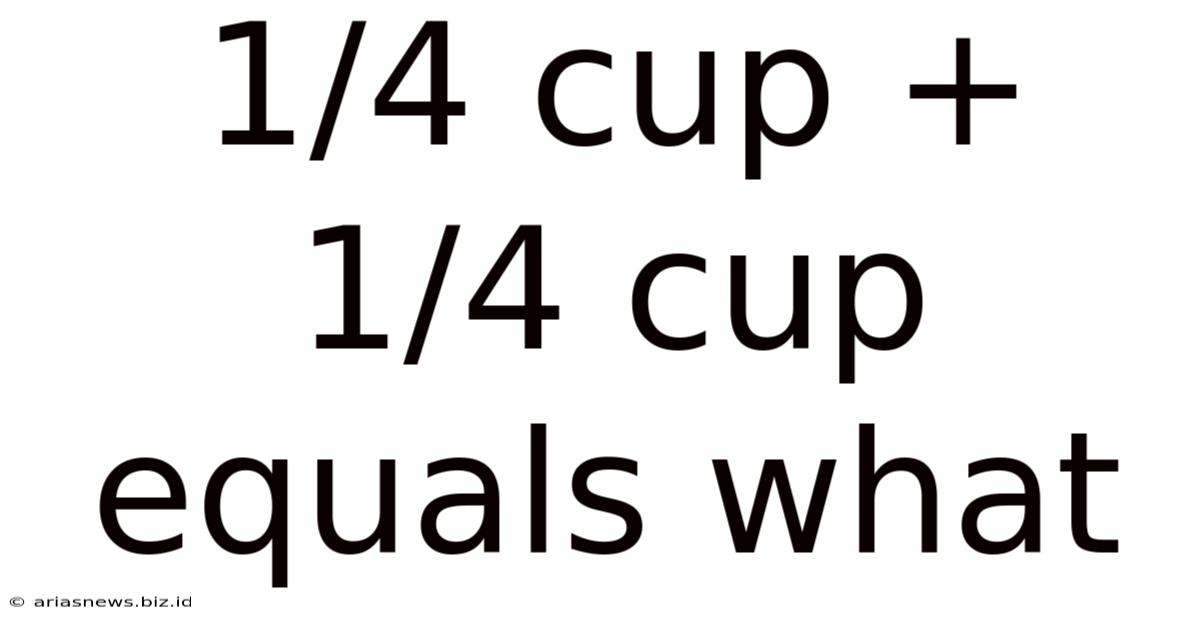
Table of Contents
1/4 Cup + 1/4 Cup Equals What: A Comprehensive Guide to Fraction Addition and Measurement
This seemingly simple question, "1/4 cup + 1/4 cup equals what?", opens the door to a deeper understanding of fractions, essential for various aspects of life, from cooking and baking to construction and even finance. While the answer is straightforward for many, understanding the underlying principles solidifies the foundation for more complex mathematical operations. This comprehensive guide explores this seemingly simple equation, providing a detailed explanation suitable for all levels of mathematical understanding.
Understanding Fractions: The Building Blocks
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number represents the number of parts you have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
In our case, 1/4 represents one part out of four equal parts. Visualizing this with a pie chart or a segmented circle can be incredibly helpful, particularly for beginners.
Adding Fractions with the Same Denominator
Adding fractions with the same denominator (the bottom number) is relatively straightforward. You simply add the numerators (the top numbers) and keep the denominator the same. This principle is fundamental to solving "1/4 cup + 1/4 cup equals what?".
1/4 + 1/4 = (1 + 1) / 4 = 2/4
Therefore, 1/4 cup + 1/4 cup equals 2/4 cups.
Simplifying Fractions: Reducing to the Lowest Terms
While 2/4 is a correct answer, it's not in its simplest form. Simplifying fractions means reducing them to their lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. In this case, the GCD of 2 and 4 is 2.
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
So, the simplified answer to 1/4 cup + 1/4 cup equals 1/2 cup.
Practical Applications: Cooking, Baking, and Beyond
Understanding fraction addition is crucial in various real-world scenarios. Consider these examples:
-
Cooking and Baking: Recipes frequently use fractions. Adding 1/4 cup of flour and another 1/4 cup necessitates understanding fraction addition to accurately measure ingredients. Incorrect measurements can significantly impact the final product's taste and texture.
-
Construction and Measurement: Many construction projects involve precise measurements. Adding fractional lengths of wood or calculating material quantities requires proficiency in fraction addition and simplification.
-
Finance and Budgeting: Understanding fractions is helpful in managing personal finances. Calculating percentages, dividing expenses, and understanding parts of a whole are all applications of fractional arithmetic.
-
Science and Engineering: Fractions are integral to many scientific and engineering calculations, from calculating chemical ratios to analyzing data.
Adding Fractions with Different Denominators: A More Advanced Approach
While the initial problem involved fractions with the same denominator, let's extend our knowledge to tackle adding fractions with different denominators. This involves finding a common denominator—a number divisible by both denominators.
For example, let's add 1/3 cup and 1/4 cup. The least common multiple (LCM) of 3 and 4 is 12. We convert each fraction to an equivalent fraction with a denominator of 12:
- 1/3 = (1 x 4) / (3 x 4) = 4/12
- 1/4 = (1 x 3) / (4 x 3) = 3/12
Now, we can add the fractions:
4/12 + 3/12 = (4 + 3) / 12 = 7/12
Therefore, 1/3 cup + 1/4 cup equals 7/12 cups. This example highlights the importance of finding a common denominator before adding fractions.
Beyond the Basics: Mixed Numbers and Improper Fractions
Let's delve further into more complex fractional arithmetic involving mixed numbers (a whole number and a fraction, like 1 1/2) and improper fractions (where the numerator is larger than the denominator, like 5/4).
Adding Mixed Numbers:
To add mixed numbers, add the whole numbers separately and then add the fractions. If the fraction sum is an improper fraction, convert it to a mixed number and add it to the whole number sum.
For example: 1 1/4 + 2 1/2
- Add the whole numbers: 1 + 2 = 3
- Find a common denominator for the fractions (4): 1/4 + 2/4 = 3/4
- Combine: 3 + 3/4 = 3 3/4
Adding Improper Fractions:
Convert improper fractions to mixed numbers before adding them or add them directly and then convert the result to a mixed number.
For example: 5/4 + 7/4 = 12/4 = 3
or converting to mixed numbers first: 1 1/4 + 1 3/4 = 3
Practical Applications of Mixed Numbers and Improper Fractions
The application of mixed numbers and improper fractions extends to various fields:
- Construction: Calculating material quantities often involves mixed numbers (e.g., 2 1/2 feet of lumber).
- Engineering: Designing structures and systems frequently requires precise calculations using fractions and mixed numbers.
- Finance: Calculating interest rates and compound interest may involve complex fractional calculations.
Troubleshooting Common Mistakes in Fraction Addition
Several common mistakes can hinder accurate fraction addition. Let's address some of them:
-
Forgetting to find a common denominator: This is the most frequent error when adding fractions with different denominators. Always ensure you have a common denominator before adding the numerators.
-
Incorrectly simplifying fractions: Failing to reduce fractions to their lowest terms can lead to inaccurate results and make further calculations more complex.
-
Adding denominators: Remember, you only add the numerators; the denominator remains the same when adding fractions with the same denominator.
-
Improper handling of mixed numbers: Adding mixed numbers requires careful attention to both the whole numbers and the fractions. Make sure to convert any improper fractions to mixed numbers before combining.
Conclusion: Mastering Fractions for a Brighter Future
While the simple question, "1/4 cup + 1/4 cup equals what?" might seem trivial at first, it serves as a gateway to understanding fractions—a fundamental concept with wide-ranging applications. Mastering fraction addition and related concepts empowers individuals to tackle more complex mathematical problems and successfully navigate various real-world scenarios, from cooking and baking to more intricate calculations in construction, engineering, and finance. This comprehensive guide equips you with the knowledge to confidently tackle fractional arithmetic and apply it effectively in your daily life. Remember to practice regularly to reinforce your understanding and build confidence in solving fractional equations. Consistent practice will make you a fraction master in no time.
Latest Posts
Latest Posts
-
Is 72 A Prime Number Or A Composite Number
May 09, 2025
-
How Much Is 1 75 Liters In Ml
May 09, 2025
-
What Are The Conflicts In The Giver
May 09, 2025
-
5 Saturdays 5 Sundays And 5 Mondays
May 09, 2025
-
How Many Yards Are In 200 Ft
May 09, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Cup + 1/4 Cup Equals What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.