1 4 Cup Plus 1 2 Cup Equals
Arias News
May 09, 2025 · 6 min read
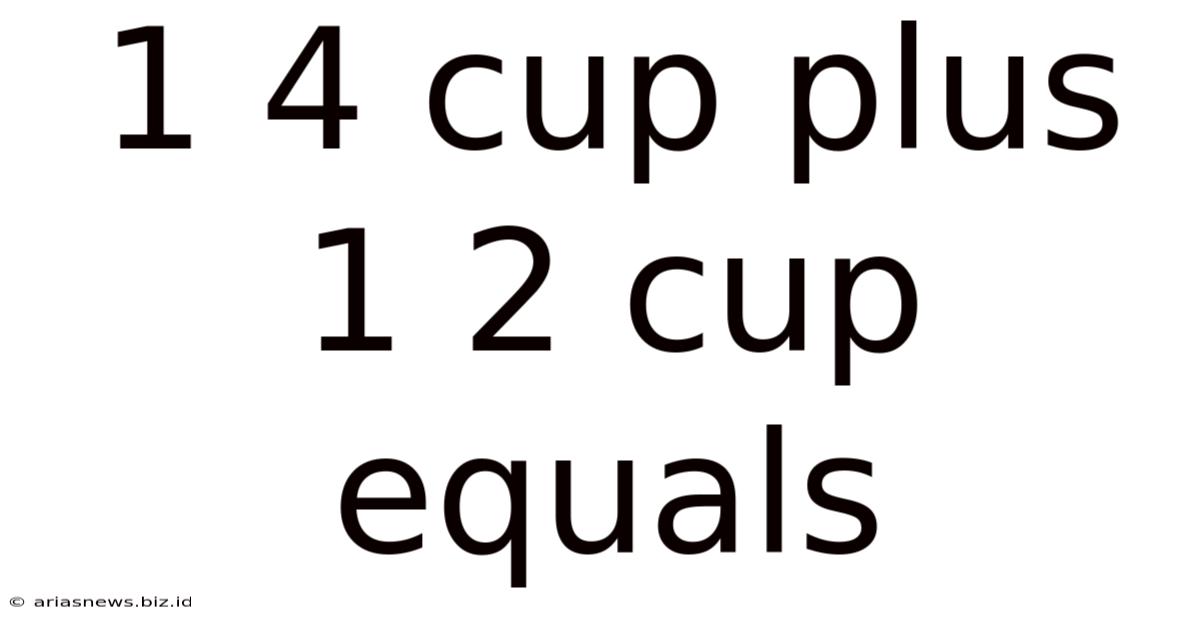
Table of Contents
1 ¼ Cup Plus ½ Cup Equals: A Comprehensive Guide to Fraction Addition in Cooking
Cooking is a science, and like any science, it requires precision. Accurate measurements are crucial for achieving the desired texture, taste, and overall success of any recipe. One common challenge for many home cooks involves understanding and correctly calculating fractional measurements. This article delves into the seemingly simple yet surprisingly nuanced question: 1 ¼ cup plus ½ cup equals? We'll explore the solution, examine the underlying mathematical principles, and provide practical applications for your culinary endeavors.
Understanding Fractions: The Foundation of Measurement
Before diving into the specific calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
In our case, we're dealing with cups, a common unit of volume in cooking. Understanding fractions is vital because many recipes call for fractional amounts of ingredients, like flour, sugar, or milk.
-
½ cup (one-half cup): This means the whole cup is divided into two equal parts, and we are using one of those parts.
-
¼ cup (one-quarter cup): This represents one out of four equal parts of a whole cup.
-
1 ¼ cups (one and one-quarter cups): This signifies one whole cup plus one-quarter of a cup.
Adding Fractions: A Step-by-Step Guide
To solve 1 ¼ cup + ½ cup, we need to add fractions with different denominators. Here's a step-by-step guide:
Step 1: Find a Common Denominator
The key to adding fractions is to ensure they share the same denominator. In our example, we have ¼ and ½. The least common denominator (LCD) for 4 and 2 is 4. This means we need to convert ½ into an equivalent fraction with a denominator of 4.
Step 2: Convert Fractions to Equivalent Fractions
To convert ½ to a fraction with a denominator of 4, we multiply both the numerator and the denominator by 2:
(½) x (2/2) = 2/4
This doesn't change the value of the fraction; it simply represents it differently.
Step 3: Add the Fractions
Now that both fractions have the same denominator, we can add them:
1 ¼ + ½ becomes 1 ¼ + 2/4
Adding the fractional parts: ¼ + 2/4 = 3/4
Step 4: Combine the Whole Number and Fraction
Combine the whole number (1) and the resulting fraction (3/4) to get the final answer:
1 ¾ cups
Therefore, 1 ¼ cup plus ½ cup equals 1 ¾ cups.
Practical Applications in Cooking
This seemingly basic calculation holds significant weight in the culinary world. Inaccurate measurements can lead to a variety of problems:
-
Incorrect Texture: Too much or too little of a specific ingredient can drastically alter the texture of baked goods, sauces, or other dishes. For instance, adding too much flour to a cake batter can result in a dry and crumbly cake.
-
Imbalanced Flavors: Precise measurements are essential for achieving the right balance of flavors. An excess of a particular spice or seasoning can overpower the other ingredients, ruining the dish's intended taste profile.
-
Failed Recipes: In extreme cases, inaccurate measurements can lead to a complete failure of the recipe, resulting in wasted ingredients and time.
Let's explore some real-world cooking examples where understanding fractional addition is crucial:
Example 1: Baking a Cake
A cake recipe might call for 1 ¼ cups of flour and ½ cup of sugar. Knowing that 1 ¼ cup + ½ cup = 1 ¾ cups, you can easily calculate the total amount of dry ingredients required for the recipe.
Example 2: Making a Sauce
A sauce recipe may require ½ cup of tomato paste and 1 ¼ cups of crushed tomatoes. Understanding fractional addition enables you to precisely measure the total amount of tomatoes needed for the sauce.
Example 3: Scaling Recipes
Many recipes can be easily scaled up or down. If you want to double a recipe that calls for 1 ¼ cups of an ingredient, simply multiply this amount by 2, which is equivalent to adding the amount to itself. This understanding empowers you to tailor recipes to the number of servings required.
Beyond Basic Addition: More Complex Scenarios
The principle of finding a common denominator and then adding the numerators extends to more complex fraction problems. For instance:
-
Adding multiple fractions: If a recipe calls for ¼ cup, ⅓ cup, and ½ cup of different ingredients, you'd need to find a common denominator for 4, 3, and 2 (which is 12) and then add the fractions.
-
Subtracting fractions: Similar to addition, subtracting fractions requires finding a common denominator. You then subtract the numerators. This might apply if you need to remove a portion of an ingredient from a larger quantity.
Mastering Fractions: A Key to Culinary Success
The ability to confidently add and subtract fractions is a fundamental skill for any serious cook. It's not just about following recipes accurately; it’s about understanding the why behind the measurements. This understanding unlocks culinary creativity, allowing you to adjust recipes, experiment with new flavors, and confidently produce delicious and consistent results every time. While technology offers many digital measuring tools, the underlying understanding of fractions remains the cornerstone of accurate cooking. Mastering this skill ensures you’ll be well-equipped to tackle any culinary challenge with precision and confidence.
Frequently Asked Questions (FAQs)
Q: What if I don't have a measuring cup that shows ¼ cup increments?
A: You can use a standard measuring cup and estimate ¼ cup. Many recipes provide alternative methods, such as using tablespoons (1 tablespoon = 1/16 cup) to achieve precise measurements when needed.
Q: Can I use a kitchen scale instead of measuring cups?
A: Yes, using a kitchen scale can offer a highly accurate way to measure ingredients, particularly for dry ingredients like flour and sugar. Many recipes now include weight measurements alongside volume measurements for greater precision.
Q: Are there any online tools or apps to help with fraction calculations?
A: Yes, many free online calculators and apps are available that can easily perform fraction calculations, providing a quick and reliable way to check your work or solve more complex problems. However, understanding the underlying mathematical concepts remains crucial for a deeper understanding of culinary precision.
This article provides a comprehensive guide to understanding and applying fractional addition in cooking, focusing on the practical implications and broader applications in the kitchen. Remember, precision is key to culinary success, and mastering fractions is a vital step on your journey to becoming a confident and skilled cook.
Latest Posts
Latest Posts
-
After Katniss Suggested An Alliance Rue Said She Could
May 11, 2025
-
Find The Greatest Common Factor Of 110 40 And 120
May 11, 2025
-
How To Reheat Chicken Parm In Oven
May 11, 2025
-
Cif Number In Central Bank Of India
May 11, 2025
-
How To Say Thank You In Afrikaans
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Cup Plus 1 2 Cup Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.