1 8 Cup Plus 1 8 Cup Equals
Arias News
May 11, 2025 · 5 min read
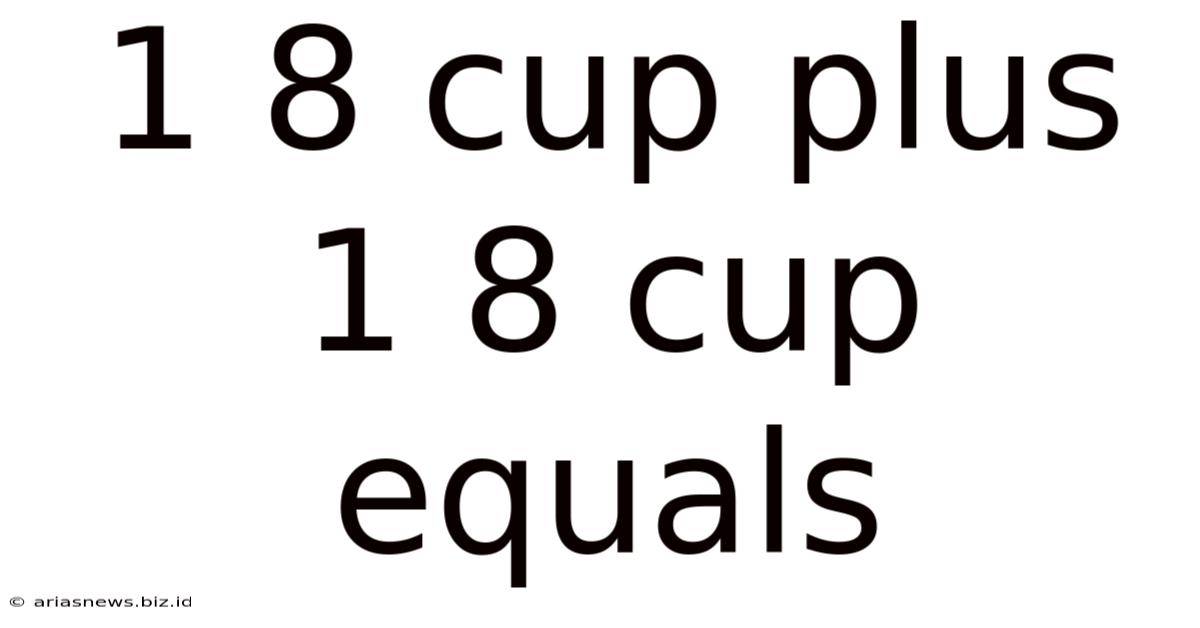
Table of Contents
1/8 Cup Plus 1/8 Cup Equals: A Deep Dive into Fractions and Measurement
This seemingly simple question, "1/8 cup plus 1/8 cup equals?", opens a door to a world of mathematical concepts, practical applications in cooking and baking, and even the importance of precise measurement in various fields. While the answer is straightforward for those familiar with fractions, understanding the underlying principles provides a solid foundation for more complex calculations and problem-solving.
Understanding Fractions: The Building Blocks of Measurement
Before diving into the addition of fractions, let's establish a firm grasp on what fractions represent. A fraction signifies a part of a whole. In the case of 1/8 cup, the whole is the cup, and the fraction indicates one out of eight equal parts of that whole. The number on the top (1) is the numerator, representing the number of parts we have. The number on the bottom (8) is the denominator, representing the total number of equal parts the whole is divided into.
Visualizing Fractions: A Simple Approach
Imagine a pie cut into eight equal slices. Each slice represents 1/8 of the whole pie. If you take two of those slices, you have 2/8 of the pie. This visual representation makes understanding fractions more intuitive, particularly when dealing with addition and subtraction.
Adding Fractions: A Step-by-Step Guide
Adding fractions with the same denominator (the bottom number) is remarkably simple. You simply add the numerators (the top numbers) and keep the denominator the same.
1/8 cup + 1/8 cup = (1 + 1)/8 = 2/8 cup
Therefore, 1/8 cup plus 1/8 cup equals 2/8 cup.
Simplifying Fractions: Reducing to Lowest Terms
While 2/8 is a correct answer, it's not in its simplest form. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 2 and 8 is 2.
2/8 ÷ 2/2 = 1/4
Thus, 2/8 cup simplifies to 1/4 cup. This is the most concise and commonly used representation of the answer.
The Importance of Precision in Cooking and Baking
In culinary arts, accurate measurements are paramount. Whether you're a seasoned chef or a novice baker, understanding fractions and their implications is critical for achieving consistent and desirable results. A slight deviation in measurements can significantly impact the texture, taste, and overall quality of your culinary creations.
Recipes and Fractional Measurements: A Common Occurrence
Many recipes call for fractional measurements, particularly when dealing with ingredients like spices, extracts, or leavening agents. A difference of even 1/8 cup can alter the outcome of a recipe, leading to a cake that's too dry, a sauce that's too thick, or cookies that spread too thin.
Baking Science: Understanding the Role of Ingredients
The precise amounts of ingredients play a crucial role in the chemical reactions that occur during baking. For example, the ratio of baking soda to baking powder impacts the rise of a cake, and the amount of liquid affects the texture. Precise measurements are fundamental to successful baking.
Beyond the Kitchen: Applications in Other Fields
The concept of adding fractions and understanding precise measurements extends far beyond cooking and baking. It's essential in various fields, including:
- Engineering: Engineers constantly work with precise measurements and calculations involving fractions. From constructing buildings and bridges to designing intricate machinery, accuracy is paramount.
- Construction: Accurate measurements are vital in construction, ensuring structures are built to specifications and remain stable and safe. Fractions are frequently used in blueprints and measurements.
- Manufacturing: In manufacturing, the precision of measurements is essential for producing high-quality products that meet stringent standards. Fractions are routinely used in production processes.
- Science: In scientific experiments and research, precise measurements are crucial for obtaining reliable and reproducible results. Understanding fractions and other mathematical concepts is fundamental in scientific work.
- Medicine: In medicine, precise measurements of dosage and quantities are essential for patient safety and treatment effectiveness. Fractions play a significant role in pharmaceutical calculations.
Expanding on Fractional Addition: More Complex Scenarios
While adding 1/8 cup and 1/8 cup is straightforward, more complex scenarios may involve fractions with different denominators. In these cases, finding a common denominator is crucial before adding the fractions.
Finding a Common Denominator: The Key to Adding Unlike Fractions
For example, adding 1/8 cup and 1/4 cup requires finding a common denominator. Since 8 is a multiple of 4, the common denominator is 8. To convert 1/4 to an equivalent fraction with a denominator of 8, we multiply both the numerator and denominator by 2:
1/4 * 2/2 = 2/8
Now we can add the fractions:
1/8 + 2/8 = 3/8
Therefore, 1/8 cup plus 1/4 cup equals 3/8 cup.
Working with Mixed Numbers: Combining Whole Numbers and Fractions
Sometimes, recipes or calculations might involve mixed numbers – numbers that combine a whole number and a fraction. For example, adding 1 1/2 cups and 1/4 cup requires converting the mixed number to an improper fraction (a fraction where the numerator is greater than the denominator) before adding.
1 1/2 = (1 * 2 + 1)/2 = 3/2
Now we find a common denominator (4) and convert the fractions:
3/2 * 2/2 = 6/4
1/4 = 1/4
Then we add the fractions:
6/4 + 1/4 = 7/4
Finally, we convert the improper fraction back to a mixed number:
7/4 = 1 3/4
Therefore, 1 1/2 cups plus 1/4 cup equals 1 3/4 cups.
Mastering Fractions: A Foundation for Mathematical Proficiency
Understanding fractions is a cornerstone of mathematical proficiency, impacting various aspects of life, from everyday tasks to specialized professions. The simple addition of 1/8 cup plus 1/8 cup serves as a gateway to exploring more complex concepts and applications, emphasizing the importance of precise measurement and mathematical understanding. Whether in the kitchen or beyond, mastering fractions empowers us to solve problems, make accurate calculations, and achieve our goals with confidence and precision.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 8 Cup Plus 1 8 Cup Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.