1 Less Than Twice The Square Of A Number
Arias News
May 11, 2025 · 5 min read
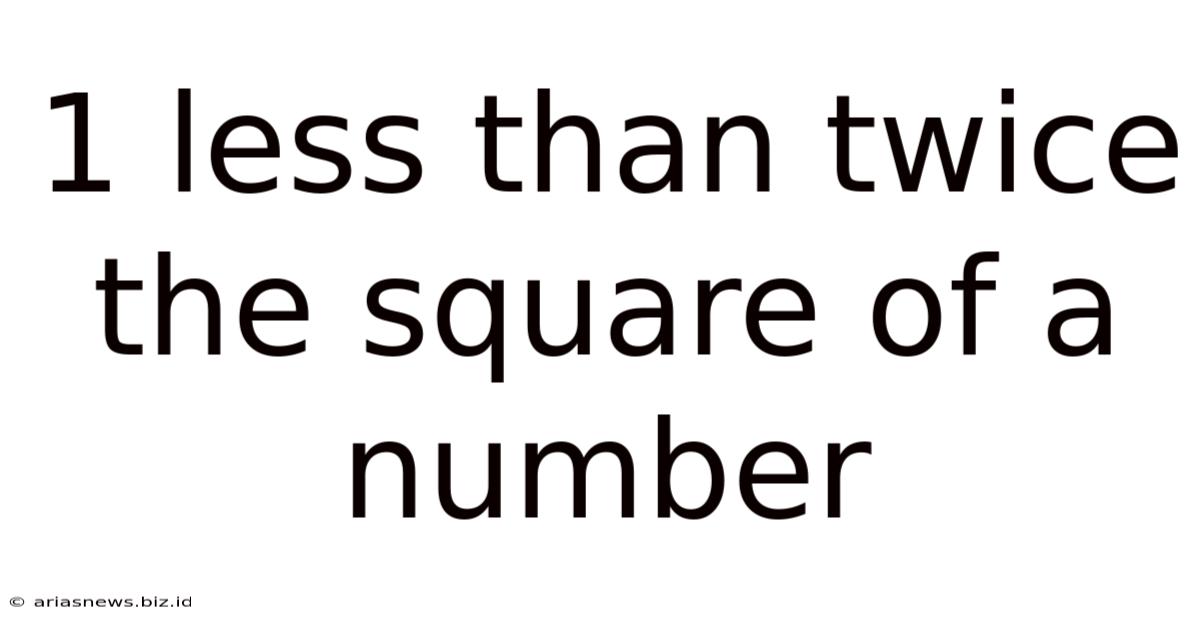
Table of Contents
1 Less Than Twice the Square of a Number: A Deep Dive into Mathematical Expressions
The seemingly simple phrase "1 less than twice the square of a number" hides a rich tapestry of mathematical concepts. This seemingly straightforward expression opens doors to exploring algebraic manipulation, equation solving, quadratic functions, and even the fascinating world of number theory. This article will delve into each aspect, providing a comprehensive understanding of this expression and its implications.
Understanding the Expression
Let's break down the expression step-by-step:
- A number: We'll represent this unknown number with the variable x.
- The square of a number: This translates to x².
- Twice the square of a number: This becomes 2x².
- 1 less than twice the square of a number: Finally, we arrive at the complete expression: 2x² - 1.
This algebraic expression, 2x² - 1, represents a quadratic function. Understanding quadratic functions is crucial to grasping the full potential of this expression.
Quadratic Functions: A Primer
A quadratic function is a polynomial function of degree two. It's generally represented in the form: f(x) = ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. Our expression, 2x² - 1, fits this form perfectly, with a = 2, b = 0, and c = -1.
The graph of a quadratic function is a parabola. The parabola's shape (opening upwards or downwards) is determined by the value of a. If a > 0 (as in our case), the parabola opens upwards; if a < 0, it opens downwards. The vertex of the parabola represents the minimum or maximum value of the function.
In our expression, 2x² - 1, the parabola opens upwards, indicating that the function has a minimum value. This minimum value occurs at the vertex of the parabola. The x-coordinate of the vertex is given by -b / 2a. Since b = 0 in our case, the x-coordinate of the vertex is 0. Substituting this into the function, we find the minimum value to be -1.
Solving Equations Involving the Expression
Now, let's explore how to solve equations involving our expression, 2x² - 1. A common type of problem might involve setting the expression equal to a specific value and solving for x. For example:
2x² - 1 = 7
To solve this equation:
- Add 1 to both sides: 2x² = 8
- Divide both sides by 2: x² = 4
- Take the square root of both sides: x = ±2
This shows that there are two solutions: x = 2 and x = -2. This is typical for quadratic equations; they often have two solutions. However, some quadratic equations may have only one solution (a repeated root) or no real solutions (when the discriminant is negative).
Let's consider another example:
2x² - 1 = -1
Following the same steps:
- Add 1 to both sides: 2x² = 0
- Divide both sides by 2: x² = 0
- Take the square root of both sides: x = 0
In this case, there is only one solution: x = 0.
Exploring the Expression's Properties
The expression 2x² - 1 exhibits several interesting mathematical properties:
- Even Function: The expression is an even function because f(-x) = f(x). This means the graph of the function is symmetric about the y-axis.
- Continuous Function: The expression is a continuous function, meaning there are no breaks or jumps in its graph.
- Range: The range of the function is [-1, ∞), meaning the function's values can be any real number greater than or equal to -1.
- Domain: The domain of the function is all real numbers (-∞, ∞).
Applications and Further Exploration
The expression "1 less than twice the square of a number" finds applications in various fields, including:
- Physics: Quadratic equations often describe projectile motion, where the height of an object as a function of time might be represented by a quadratic expression similar to ours.
- Engineering: Quadratic equations are fundamental to many engineering problems, such as calculating the strength of materials or designing optimal structures.
- Economics: Quadratic functions can model various economic phenomena, such as cost functions or profit maximization.
- Computer Science: Quadratic functions are used in algorithms and data structures.
Further exploration could involve:
- Calculus: Analyzing the expression using calculus techniques like finding the derivative and integral. The derivative would reveal the slope of the tangent line at any point on the parabola, while the integral would represent the area under the curve.
- Number Theory: Investigating the properties of the expression when x is restricted to specific types of numbers, such as integers or prime numbers. Are there any patterns or relationships that emerge?
- Complex Numbers: Extending the domain of the expression to include complex numbers and analyzing the resulting behavior.
Conclusion
The seemingly simple expression "1 less than twice the square of a number," or 2x² - 1, opens a window into the rich world of mathematics. From understanding its algebraic structure and solving equations to exploring its properties and applications, the expression provides endless opportunities for learning and discovery. This deep dive has hopefully illuminated the diverse facets of this seemingly simple expression, showcasing its significance and potential for further exploration within various mathematical disciplines. By understanding this expression, we gain valuable insights into the broader world of quadratic functions and their importance in diverse fields. The exploration of this expression serves as a microcosm of mathematical investigation – a journey from the specific to the general, from the simple to the complex.
Latest Posts
Latest Posts
-
Elevated Trains And Subways Improved Travel By
May 12, 2025
-
43 Out Of 48 As A Percentage
May 12, 2025
-
How To Remove Dried Mod Podge From Plastic
May 12, 2025
-
10 Gallon Hat Holds How Much Water
May 12, 2025
-
How Many Generations From Adam To Moses
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1 Less Than Twice The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.