10 Times As Many As 1 Hundred Is
Arias News
Mar 31, 2025 · 5 min read
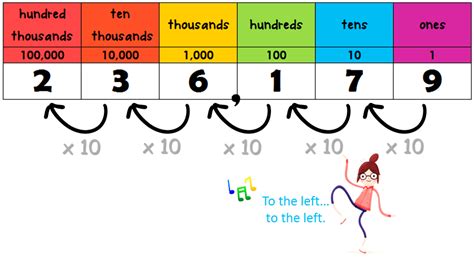
Table of Contents
10 Times as Many as 1 Hundred Is: Exploring Multiplication and its Applications
Understanding multiplication is fundamental to mathematics and its applications span across numerous fields. This article delves into the simple yet crucial concept of "10 times as many as 1 hundred is," exploring its meaning, practical applications, and expanding upon the broader principles of multiplication. We'll unpack this seemingly basic concept, revealing its significance in various contexts and showing how it forms a building block for more complex mathematical operations.
Deconstructing the Problem: 10 Times as Many as 1 Hundred
The statement "10 times as many as 1 hundred is" essentially poses a multiplication problem. It asks us to find the product of 10 and 100. In mathematical notation, this is represented as:
10 x 100 = ?
The solution is straightforward: 10 multiplied by 100 equals 1000. Therefore, 10 times as many as 1 hundred is 1000.
However, understanding this calculation goes beyond simply finding the answer. It's about grasping the concept of multiplication itself and how it reflects real-world scenarios.
Understanding Multiplication: Repeated Addition
Multiplication can be viewed as repeated addition. In this case, "10 times as many as 100" means adding 100 to itself 10 times:
100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + 100 = 1000
This visual representation clarifies the meaning of multiplication and its relationship to addition. While repeated addition is suitable for smaller numbers, multiplication provides a far more efficient way to solve larger problems.
Practical Applications: Where This Concept Matters
The concept of "10 times as many as 1 hundred" isn't confined to the abstract realm of mathematics; it finds practical application in numerous real-world scenarios.
1. Business and Finance:
- Inventory Management: A company might have 100 units of a particular product in stock. If they order 10 times as many, they'll receive 1000 units.
- Sales Projections: If a business makes a profit of $100 in a day, projecting 10 times that amount helps them forecast potential earnings over a longer period.
- Investment Growth: If an investment grows by 100% in a year, and that growth continues for another 10 years at that rate, understanding exponential growth (100 x 10) becomes crucial for assessing long-term returns.
2. Everyday Life:
- Counting Objects: Imagine 10 bags, each containing 100 marbles. To find the total number of marbles, you would calculate 10 x 100 = 1000.
- Measurement Conversions: Converting units often involves multiplication. For example, if 1 meter equals 100 centimeters, then 10 meters would equal 1000 centimeters (10 x 100).
- Recipe Scaling: Doubling or tripling a recipe involves multiplication. If a recipe calls for 100 grams of flour, multiplying by 10 would result in 1000 grams of flour needed for a larger batch.
3. Science and Engineering:
- Data Analysis: Scientists often deal with large datasets. If a researcher collects 100 data points per experiment and conducts 10 experiments, they would have 1000 data points to analyze.
- Engineering Calculations: Construction and other engineering disciplines use multiplication extensively in calculations involving materials, measurements, and structural design.
4. Education:
- Problem Solving: This simple multiplication problem provides a foundational understanding for tackling more complex mathematical problems in algebra, geometry, and calculus.
- Developing Number Sense: Repeated exposure to problems like this helps students develop a strong intuition for numbers and their relationships.
Expanding the Concept: Beyond 10 and 100
While the example focuses on 10 and 100, the underlying principle applies to any multiplication problem. Let's explore how this concept extends to other numbers and situations:
-
Different Multipliers: Instead of 10, consider multiplying 100 by other numbers: 5 x 100 = 500, 20 x 100 = 2000, 100 x 100 = 10,000, and so on. The same principle applies: the result is the product of the two numbers.
-
Different Multiplicands: Instead of 100, consider multiplying different numbers by 10: 10 x 50 = 500, 10 x 250 = 2500, etc. This shows how the multiplier (10) scales the multiplicand.
-
Real-world Variations: The applications extend far beyond simple counting. For instance, consider calculating the total cost of 10 items each priced at $100 or the area of a rectangle measuring 10 units by 100 units.
Mastering Multiplication: Strategies and Techniques
Developing proficiency in multiplication is crucial for mathematical success. Several strategies can improve one's understanding and speed:
-
Memorization: Learning multiplication tables (times tables) is fundamental. Knowing these facts by heart significantly speeds up calculations.
-
Practice: Consistent practice is essential. Solving various multiplication problems regularly helps build familiarity and fluency.
-
Visual Aids: Using visual aids like number lines, arrays (rectangular arrangements of objects), or diagrams can help visualize multiplication as repeated addition.
-
Breaking Down Problems: Complex multiplication problems can be broken down into smaller, simpler problems. For instance, 15 x 100 can be solved by calculating (10 x 100) + (5 x 100).
-
Using Calculators (Strategically): While calculators are useful tools, it's important to develop a strong understanding of the underlying mathematical principles before relying solely on them. Calculators should be used for checking answers or tackling very large numbers.
Connecting Multiplication to Other Mathematical Concepts
Understanding "10 times as many as 1 hundred" forms a cornerstone for more advanced mathematical concepts:
-
Exponents: This concept relates directly to exponents. 10 x 100 can be expressed as 10¹ x 10² = 10³. This introduces the idea of exponential growth.
-
Algebra: In algebra, this concept translates into solving equations involving variables. For example, 10x = 1000 can be solved to find the value of x.
-
Geometry: Calculating areas and volumes often involves multiplication. The area of a rectangle is length x width.
Conclusion: The Enduring Importance of Multiplication
The seemingly simple problem of "10 times as many as 1 hundred is" highlights the fundamental importance of multiplication in mathematics and its widespread applications in everyday life, various professions, and advanced scientific fields. Mastering this concept not only enhances numerical skills but also lays the foundation for tackling more complex mathematical challenges and understanding the world around us more effectively. By understanding the principles of multiplication and utilizing effective learning strategies, individuals can build a strong foundation in mathematics and apply this knowledge to solve a wide range of problems, ultimately contributing to greater success in academic and professional endeavors. The more deeply we understand this basic concept, the more confidently we can approach increasingly complex mathematical tasks.
Latest Posts
Latest Posts
-
How Much Does A Gallon Of Mayonnaise Weigh
Apr 02, 2025
-
How Much Protein Is In An 8 Oz Chicken Breast
Apr 02, 2025
-
Which Is The Most Plausible Theme In The Raven
Apr 02, 2025
-
10 Cm X 10 Cm X 10 Cm
Apr 02, 2025
-
How Many Dollars Is 1 Billion Pennies
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 10 Times As Many As 1 Hundred Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
