10 To The Negative Power Of 2
Arias News
May 10, 2025 · 5 min read
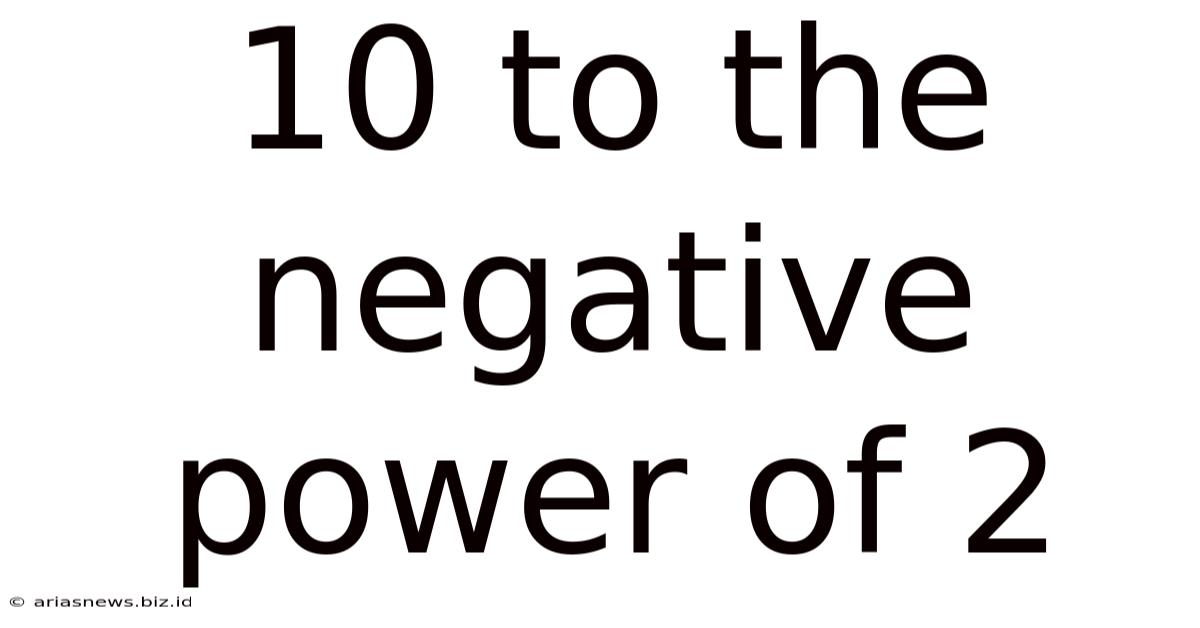
Table of Contents
10 to the Negative Power of 2: A Deep Dive into Exponential Notation and its Applications
Understanding exponential notation, particularly negative exponents, is crucial for navigating various fields, from basic arithmetic to advanced scientific calculations. This article delves deep into the concept of 10 to the negative power of 2 (10⁻²), exploring its mathematical meaning, practical applications, and relevance in different contexts. We'll move beyond a simple numerical answer and explore the broader implications of this seemingly simple concept.
What Does 10⁻² Mean?
At its core, 10⁻² represents a power of ten expressed using negative exponents. Negative exponents indicate reciprocals. In simpler terms, it's the reciprocal of 10², which is 10 multiplied by itself twice (10 * 10 = 100). Therefore, 10⁻² is equal to 1/10² = 1/100 = 0.01.
This fundamental principle applies to any base number raised to a negative power: a⁻ⁿ = 1/aⁿ. This relationship is a cornerstone of exponential algebra and is vital for understanding scientific notation and various mathematical operations.
Understanding Exponential Notation
Exponential notation provides a concise way to represent very large or very small numbers. It's particularly useful in scientific fields where dealing with extremely large or small quantities is commonplace. The general form is a × 10ᵇ, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer exponent.
The exponent 'b' indicates how many places the decimal point needs to be moved to obtain the standard form of the number. A positive 'b' signifies a large number (decimal point moves to the right), while a negative 'b' signifies a small number (decimal point moves to the left).
10⁻² in Scientific Notation and Metric Prefixes
In scientific notation, 10⁻² is a common factor used to represent the metric prefixes centi (c) and hecto (h) in reverse. While centi represents 10⁻², hecto is 10². Understanding this relationship highlights the symmetry and elegance of the metric system.
For example:
- 1 centimeter (cm) = 10⁻² meters (m) This means that one centimeter is one-hundredth of a meter.
- 100 hectometers (hm) = 10² * 10² meters (m) = 10⁴ meters (m)
This illustrates how 10⁻² forms a crucial building block within the standardized system of measurements used worldwide.
Practical Applications of 10⁻²
The application of 10⁻² extends far beyond the theoretical realm of mathematics. Its practical use spans various fields:
1. Measurements and Conversions:
As shown above, 10⁻² is inherently linked to metric conversions. Converting between meters and centimeters, for instance, requires understanding this exponential relationship. Similar conversions occur in other measurement systems, albeit with different bases.
2. Area Calculations:
Imagine calculating the area of a square with sides of 1 centimeter each. The area would be 1 cm * 1 cm = 1 cm², which is equivalent to 10⁻² m * 10⁻² m = 10⁻⁴ m². This highlights how exponents combine when dealing with multiplicative operations like area calculations.
3. Scientific Notation and Data Representation:
In scientific research, extremely small values are often encountered. For example, the concentration of a substance in a solution might be expressed using scientific notation involving 10⁻². This allows scientists to represent these tiny quantities in a manageable and easily understandable format.
4. Financial Calculations:
Financial modeling frequently involves percentages. Expressing a percentage as a decimal (e.g., 1% = 0.01 = 10⁻²) simplifies calculations involving compound interest, discounts, and other financial instruments.
5. Computer Science and Data Storage:
In computer science, the concept of bytes, kilobytes, megabytes, and so on, utilizes powers of 10 (or 2, more accurately) for data storage representation. Understanding negative exponents is essential for translating between these different units of data.
Beyond the Basics: Exploring Related Concepts
Understanding 10⁻² opens doors to comprehending more advanced mathematical and scientific concepts:
1. Logarithms:
Logarithms are the inverse function of exponentiation. The logarithm (base 10) of 0.01 is -2, reflecting the exponent in 10⁻² = 0.01. Logarithms are critical in various fields, from chemistry (pH calculations) to earthquake measurement (Richter scale).
2. Decibels:
Decibels (dB), a logarithmic unit used to measure sound intensity, pressure, and other physical quantities, frequently utilizes powers of 10, including negative exponents, to express sound levels. A decrease of 20 dB represents a reduction in sound intensity by a factor of 10⁻².
3. pH Scale:
The pH scale, used to measure acidity or alkalinity of a solution, uses a logarithmic scale based on the concentration of hydrogen ions. The pH is the negative logarithm (base 10) of the hydrogen ion concentration. A pH of 2 means a hydrogen ion concentration of 10⁻² moles per liter.
Practical Exercises to Solidify Understanding
To reinforce the concept of 10⁻², try the following exercises:
- Convert 5 centimeters to meters: This involves multiplying 5 by 10⁻².
- Calculate the area of a square with sides measuring 0.01 meters: This relates directly to the application of 10⁻² in area calculations.
- Express 0.0005 in scientific notation: This challenges the understanding of scientific notation and negative exponents.
- What is the reciprocal of 10⁻²? This tests the understanding of reciprocal relationships with negative exponents.
- If the sound intensity decreases by 20 dB, how much does it reduce in terms of intensity ratio? This probes the application of 10⁻² in logarithmic scales.
Conclusion
10⁻² is more than just a simple numerical value; it's a fundamental building block in various mathematical and scientific fields. Understanding its meaning, implications, and applications is crucial for anyone seeking a solid grasp of exponential notation and its practical relevance in various disciplines. This exploration aims not only to clarify the concept of 10⁻² but also to highlight its wider significance within the broader landscape of mathematics and science. By exploring its connections to other concepts like logarithms, scientific notation, and metric conversions, we hope to provide a comprehensive understanding that empowers you to confidently use and interpret this essential numerical concept in diverse contexts.
Latest Posts
Latest Posts
-
How Many Times Does 4 Go Into 7
May 10, 2025
-
How Do You Measure The Wheelbase On A Semi Truck
May 10, 2025
-
A Refrigerant Oil That Is Hygroscopic Is
May 10, 2025
-
How Many Bottles Of Water Equal A Liter
May 10, 2025
-
How Much Does 64 Ounces Of Water Weigh
May 10, 2025
Related Post
Thank you for visiting our website which covers about 10 To The Negative Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.