120 Out Of 140 As A Percentage
Arias News
May 12, 2025 · 5 min read
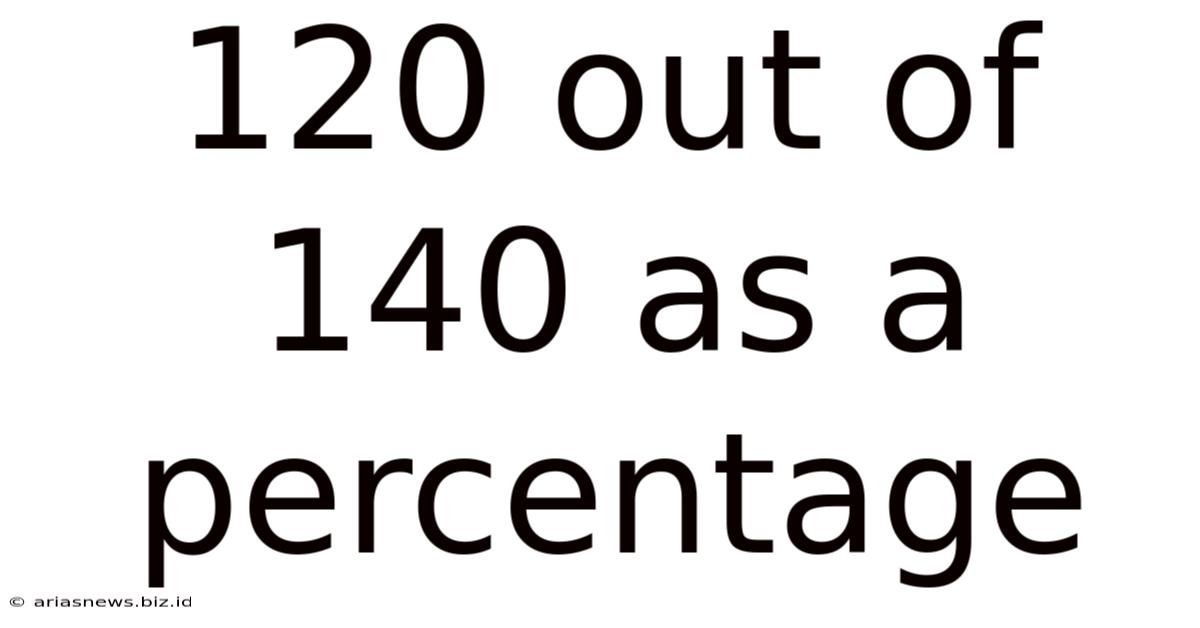
Table of Contents
120 out of 140 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and everyday problem-solving. Understanding how to determine percentages allows you to effectively analyze data, interpret results, and make informed decisions. This comprehensive guide delves into the process of calculating "120 out of 140 as a percentage," providing a step-by-step explanation, exploring different calculation methods, and offering real-world examples to solidify your understanding.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred." For instance, 50% represents 50 out of 100, or 50/100, which simplifies to 1/2.
Calculating 120 out of 140 as a Percentage: The Basic Method
The most straightforward method to calculate 120 out of 140 as a percentage involves three simple steps:
Step 1: Formulate the Fraction
First, express the given numbers as a fraction. In this case, 120 is the part, and 140 is the whole. This gives us the fraction 120/140.
Step 2: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number). In this instance:
120 ÷ 140 = 0.857142857...
Step 3: Convert the Decimal to a Percentage
Finally, multiply the decimal by 100 to express it as a percentage.
0.857142857... × 100 = 85.7142857...%
Therefore, 120 out of 140 is approximately 85.71%. Depending on the level of precision required, you can round this to 85.7% or 86%.
Alternative Calculation Methods
While the basic method is efficient, other methods can be employed depending on your preference and the tools available.
Using a Calculator
Most calculators have a percentage function. Simply enter 120 ÷ 140 and then multiply the result by 100. The calculator will automatically provide the percentage value. This is arguably the fastest and most convenient method, especially for complex calculations.
Using a Spreadsheet Software (e.g., Excel, Google Sheets)
Spreadsheet software offers built-in functions for percentage calculations. You can use the formula =120/140*100 in a cell to get the result directly. This method is particularly useful when working with large datasets or performing multiple percentage calculations.
Mental Calculation (Approximation)
For quick approximations, you can simplify the fraction. Notice that 120/140 can be simplified to 6/7 by dividing both numerator and denominator by 20. Since 6/7 is slightly less than 1 (7/7), you can estimate the percentage to be around 85-90%. This method is useful for quick checks and estimations but lacks precision.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
Academic Performance
Imagine a student scores 120 marks out of a total of 140 marks in an exam. Their percentage score, calculated as 85.71%, provides a clear indication of their performance compared to the total possible marks. This is widely used to assess student achievements in various academic settings.
Financial Calculations
Percentages are extensively used in finance. For instance, calculating interest rates, discounts, tax rates, profit margins, and investment returns all involve percentage calculations. If an item is discounted by 15%, the calculation of the final price requires percentage computations. Similarly, understanding loan interest rates necessitates calculating percentages.
Data Analysis and Interpretation
In data analysis, percentages are essential for summarizing and interpreting data. For example, if a survey shows that 120 out of 140 respondents prefer a specific product, the percentage (85.71%) provides a concise representation of the preference distribution. Percentages aid in visualizing data through charts and graphs, facilitating better communication and comprehension of insights.
Everyday Life
Many everyday situations involve percentage calculations. For example, calculating tips in restaurants, figuring out sales discounts, determining the percentage of ingredients in a recipe, or understanding nutritional labels on food products all involve percentages.
Addressing Potential Challenges and Misconceptions
While percentage calculations are generally straightforward, some common challenges and misconceptions need addressing:
Rounding Errors
Rounding numbers can introduce minor inaccuracies. When rounding to a certain number of decimal places, you might get slightly different results depending on the rounding method used (e.g., rounding up, rounding down, or rounding to the nearest). Understanding these variations is crucial for accurate interpretation.
Understanding the "Whole"
It’s important to correctly identify the "whole" or total value in the context of a problem. Mistakes often occur when the incorrect number is taken as the total, leading to erroneous percentage calculations. Always ensure you accurately identify the denominator (the whole) before starting the calculation.
Percentage Increase and Decrease
Calculating percentage increases and decreases requires a slightly different approach. To calculate the percentage increase, you find the difference between the new value and the original value, divide by the original value, and multiply by 100. Percentage decrease is calculated similarly but involves subtracting the new value from the original value.
Expanding on Percentage Concepts: Beyond the Basics
To solidify your understanding, let's explore some related percentage concepts:
Percentage Points vs. Percentage Change
It’s crucial to differentiate between percentage points and percentage change. A percentage point represents an absolute difference between two percentages, while percentage change signifies the relative difference between two values expressed as a percentage. For example, if interest rates increase from 5% to 8%, the increase is 3 percentage points, but the percentage change is 60% ((8-5)/5 * 100).
Compound Interest
Compound interest involves calculating interest on both the principal amount and accumulated interest. This type of calculation requires iterative percentage calculations, leading to exponential growth over time.
Conclusion
Calculating 120 out of 140 as a percentage, resulting in approximately 85.71%, is a simple yet powerful demonstration of percentage calculation methods. This skill is essential for various aspects of life, from academic performance evaluation to financial management and data analysis. By understanding the different calculation methods, potential challenges, and related concepts, you can confidently apply percentage calculations to solve real-world problems and make informed decisions. Remember to always double-check your work and consider the context of the problem to ensure accurate and meaningful results. The ability to confidently perform percentage calculations significantly enhances your quantitative literacy and decision-making skills.
Latest Posts
Latest Posts
-
What Does Ssa Stand For In Criminal Minds
May 12, 2025
-
How Long Can Centipedes Live Without Food
May 12, 2025
-
Can You Use Alcohol As Lighter Fluid
May 12, 2025
-
Ping Pong Ball Vs Golf Ball Size
May 12, 2025
-
Lowest Common Multiple Of 9 And 11
May 12, 2025
Related Post
Thank you for visiting our website which covers about 120 Out Of 140 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.