125 125 Is What Percent Of 50 50
Arias News
May 10, 2025 · 5 min read
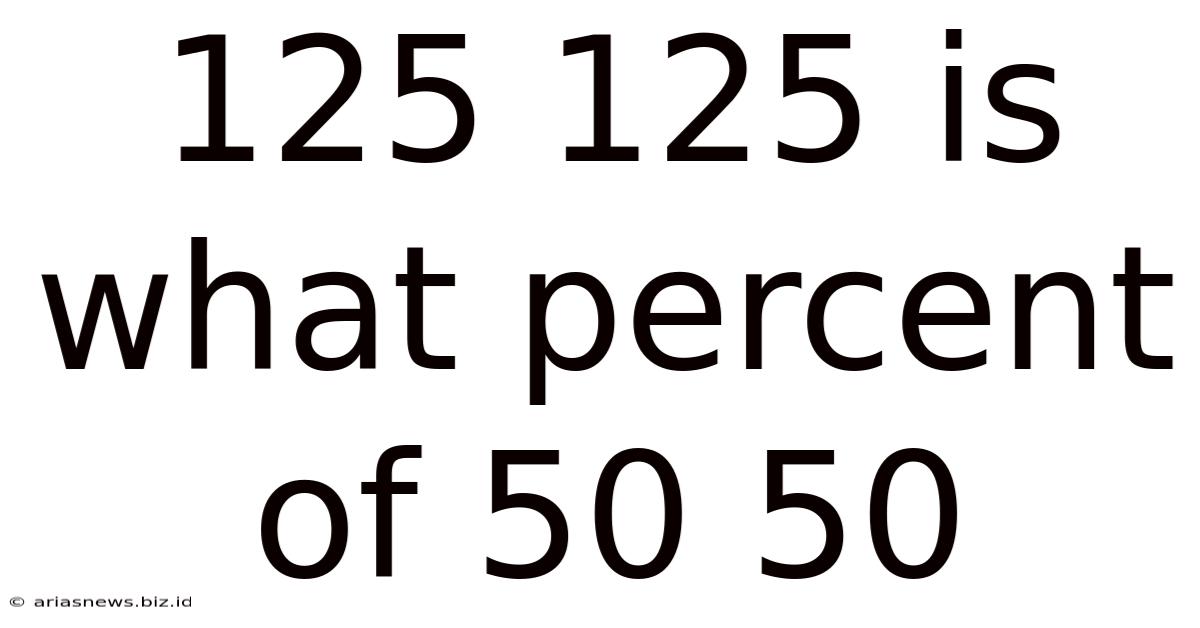
Table of Contents
125/125 is What Percent of 50/50? Understanding Percentage Calculations and Their Applications
The question, "125/125 is what percent of 50/50?" might seem deceptively simple at first glance. However, it presents a valuable opportunity to delve into the fundamentals of percentage calculations, exploring various approaches and highlighting their applications in diverse fields. This detailed guide will not only answer the question directly but also equip you with a robust understanding of percentage calculations, ensuring you can tackle similar problems with confidence.
Deconstructing the Problem: Fractions and Percentages
Before diving into the calculation, let's break down the core components:
-
125/125: This fraction represents the ratio of 125 to itself. Any number divided by itself equals 1. Therefore, 125/125 simplifies to 1.
-
50/50: Similar to the previous fraction, 50/50 simplifies to 1.
The question, therefore, transforms into: "1 is what percent of 1?"
Method 1: The Basic Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 1 (representing 125/125)
- Whole: 1 (representing 50/50)
Substituting these values into the formula:
(1 / 1) x 100% = 100%
Therefore, 125/125 is 100% of 50/50.
Method 2: Understanding Proportions
We can also approach this problem using proportions. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the percentage:
x/100 = 1/1
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
1 * x = 1 * 100
x = 100
This again confirms that 125/125 is 100% of 50/50.
Method 3: Decimal Conversion
We can convert the fractions to decimals before calculating the percentage. Both 125/125 and 50/50 equal 1.0. Therefore:
(1.0 / 1.0) x 100% = 100%
Beyond the Basics: Applying Percentage Calculations
Understanding percentage calculations extends far beyond simple mathematical problems. Their applications permeate various aspects of life, including:
1. Finance and Economics:
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, is crucial for financial planning.
-
Inflation: The rate of inflation, which measures the increase in the general price level of goods and services, is expressed as a percentage. Tracking inflation helps individuals and governments make informed economic decisions.
-
Investment Returns: The performance of investments, such as stocks and bonds, is often expressed as a percentage return on investment (ROI). ROI is calculated as (Net Profit / Cost of Investment) x 100%.
-
Taxes: Taxes are levied as a percentage of income, sales, or property value. Understanding tax rates is crucial for accurate financial planning and tax compliance.
2. Science and Engineering:
-
Data Analysis: Percentages are essential for analyzing data, representing proportions, and drawing conclusions from experimental results. Statistical analyses often rely heavily on percentage calculations.
-
Error Analysis: In scientific experiments, errors are often expressed as percentages to quantify the uncertainty in measurements. This allows scientists to assess the reliability of their results.
-
Efficiency Calculations: Engineers use percentages to express the efficiency of machines and systems. For instance, the efficiency of an engine might be expressed as the percentage of input energy converted into useful work.
3. Everyday Life:
-
Sales and Discounts: Retailers frequently advertise sales and discounts as percentages, such as "20% off." Understanding these percentages helps consumers make informed purchasing decisions.
-
Tips and Gratuities: Calculating tips in restaurants or other service industries involves using percentages. A common practice is to tip 15% or 20% of the bill.
-
Surveys and Polls: Results from surveys and polls are often presented as percentages to summarize public opinion or preferences. Understanding how percentages are used in surveys helps in interpreting data accurately.
-
Nutritional Information: Food labels often display the percentage of daily recommended values for various nutrients. This allows consumers to monitor their nutrient intake and make healthy food choices.
Advanced Percentage Concepts: Beyond the Basics
While the initial problem was straightforward, let's delve into more complex scenarios involving percentages:
1. Percentage Increase and Decrease:
Calculating percentage increases or decreases requires understanding the initial value and the change in value. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] x 100%
Similarly, the formula for percentage decrease is:
[(Old Value - New Value) / Old Value] x 100%
For example, if a product's price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
2. Percentage Points vs. Percentages:
It's crucial to distinguish between percentage points and percentages. A percentage point represents an absolute change in percentage values, while a percentage represents a relative change. For example, if the interest rate increases from 5% to 8%, the increase is 3 percentage points, but the percentage increase is 60% [(8-5)/5 * 100%].
3. Compound Interest:
Compound interest is the interest earned not only on the principal amount but also on the accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Mastering percentage calculations is a fundamental skill with far-reaching applications. While the initial problem of "125/125 is what percent of 50/50?" provided a simple introduction, this expanded explanation unveils the multifaceted nature of percentages and their significance in various fields. By understanding the different methods and their applications, you are well-equipped to confidently tackle percentage-related problems in any context.
Latest Posts
Latest Posts
-
3 Letter Words With H In The Middle
May 10, 2025
-
How Many Teaspoons Is A Gram Of Yeast
May 10, 2025
-
How Many Inches Are In A Liter
May 10, 2025
-
What Does 16 Mean In The Bible
May 10, 2025
-
Madea Big Happy Family Song At The Funeral
May 10, 2025
Related Post
Thank you for visiting our website which covers about 125 125 Is What Percent Of 50 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.