125 Out Of 200 As A Percentage
Arias News
May 10, 2025 · 4 min read
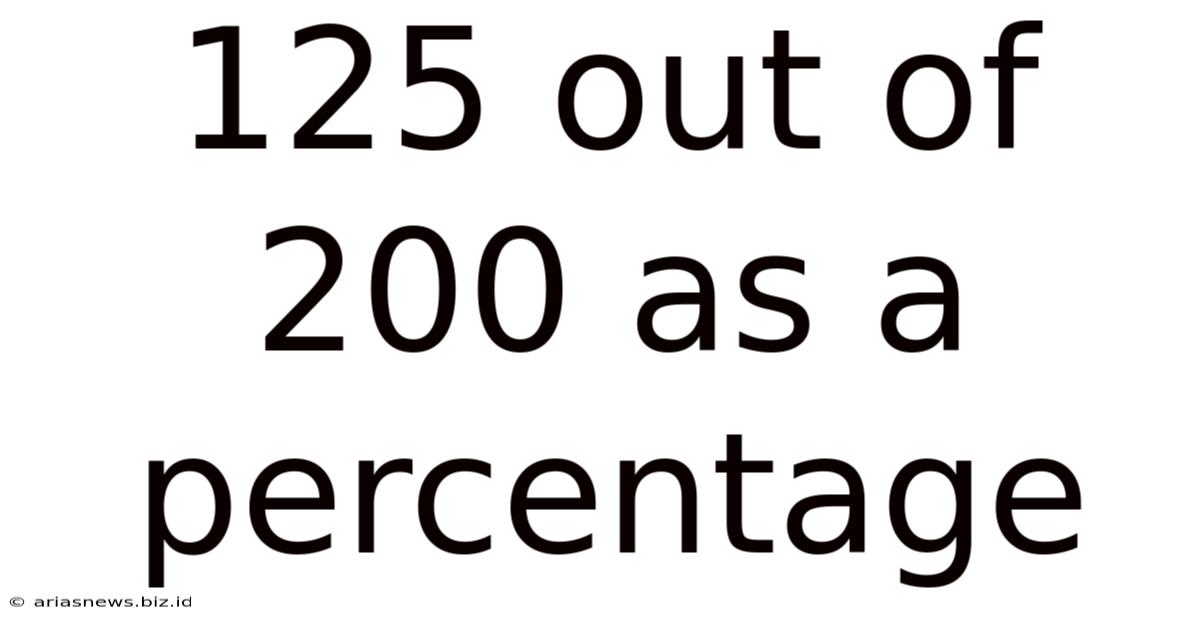
Table of Contents
125 out of 200 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to determine percentages empowers you to analyze data, make informed comparisons, and effectively communicate numerical information. This comprehensive guide delves into the calculation of "125 out of 200 as a percentage," explaining the process step-by-step, exploring different methods, and highlighting the significance of percentage calculations in diverse contexts.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100, signifying a part of a whole. The symbol "%" denotes a percentage, indicating that a number is expressed as a fraction of one hundred. For example, 50% means 50 out of 100, or one-half. Percentages provide a standardized way to compare proportions, making it easier to grasp and interpret numerical relationships.
Calculating 125 out of 200 as a Percentage: The Method
The core principle behind percentage calculation involves expressing the given values as a fraction and then converting this fraction to a percentage. In our case, we want to find out what percentage 125 represents when compared to 200.
Here's the step-by-step process:
-
Express as a Fraction: The first step is to express the given values (125 and 200) as a fraction. The part (125) forms the numerator, and the whole (200) forms the denominator:
125/200
-
Convert to Decimal: Next, convert the fraction to a decimal by dividing the numerator by the denominator:
125 ÷ 200 = 0.625
-
Convert to Percentage: To express the decimal as a percentage, multiply the decimal by 100 and add the percentage symbol (%):
0.625 × 100 = 62.5%
Therefore, 125 out of 200 is 62.5%.
Alternative Calculation Methods
While the above method is straightforward, alternative approaches can enhance understanding and provide flexibility depending on the context.
Using Proportions:
This method uses the concept of proportions to solve for the unknown percentage. We can set up a proportion:
x/100 = 125/200
Cross-multiplying and solving for 'x':
200x = 12500 x = 12500/200 x = 62.5
Therefore, x = 62.5%, confirming our previous result.
Using a Calculator:
Most calculators have a percentage function that simplifies the process. Simply input "125 ÷ 200" and then multiply the result by 100 to obtain the percentage.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in diverse situations. Here are a few examples:
-
Academic Performance: Calculating grades, analyzing test scores, and assessing overall academic performance frequently involve percentages. For instance, a student scoring 125 out of 200 on an exam achieved a 62.5% grade.
-
Financial Management: Percentages are fundamental in finance. Interest rates, discounts, tax calculations, profit margins, and investment returns are all expressed and calculated using percentages.
-
Data Analysis: Percentage calculations are essential for interpreting and analyzing data, making comparisons, and drawing meaningful conclusions. For instance, analyzing market share, survey results, and demographic trends often uses percentages.
-
Everyday Life: Percentages are routinely used in everyday situations, such as calculating tips, understanding sales discounts, and determining the proportion of ingredients in a recipe.
-
Scientific Research: In scientific studies and experiments, percentages are crucial for expressing and interpreting results, quantifying changes, and drawing conclusions.
Beyond the Basics: Advanced Percentage Calculations
While calculating "125 out of 200 as a percentage" is a straightforward application, the concept extends to more complex scenarios. Here are a few examples:
-
Percentage Increase/Decrease: Calculating the percentage change between two values involves determining the difference, dividing it by the original value, and then multiplying by 100.
-
Percentage of a Percentage: This involves calculating a percentage of a value that itself is already a percentage.
-
Compound Percentages: This deals with situations where a percentage change is applied repeatedly, such as compound interest calculations.
-
Weighted Averages: This involves calculating an average where different values have varying weights or importance, often expressed as percentages.
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and understanding of the underlying principles. Here are some tips for improving your skills:
-
Practice regularly: Work through various percentage problems, starting with simple examples and gradually increasing complexity.
-
Utilize online resources: Many websites and educational platforms offer practice problems, tutorials, and interactive exercises on percentage calculations.
-
Understand the concepts: Ensure a thorough grasp of the fundamental principles behind percentages, fractions, and decimals.
-
Apply the concepts to real-life scenarios: Relate percentage calculations to real-world situations to improve comprehension and retention.
-
Check your work: Always verify your answers using alternative methods or online calculators to ensure accuracy.
Conclusion: The Significance of Percentage Calculations
In summary, calculating "125 out of 200 as a percentage" — resulting in 62.5% — is a fundamental skill with far-reaching implications. From academic assessments to financial planning, data analysis, and everyday decision-making, understanding and applying percentage calculations is crucial. By mastering this skill, you'll enhance your ability to interpret data, make informed choices, and effectively communicate numerical information. The diverse applications of percentage calculations underscore their importance in navigating various aspects of life and achieving success in academic, professional, and personal pursuits. Continuous practice and a strong understanding of the underlying concepts will enable you to confidently handle even more complex percentage calculations in the future.
Latest Posts
Latest Posts
-
What Are The 3 Riddles Of Turandot
May 11, 2025
-
Do You Have To Go To Homecoming
May 11, 2025
-
Excuses Are Tools Of The Incompetent Meaning
May 11, 2025
-
How Much Did A Gallon Of Milk Cost In 1959
May 11, 2025
-
Boiling Point And Freezing Point Of Water In Celsius
May 11, 2025
Related Post
Thank you for visiting our website which covers about 125 Out Of 200 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.