15 Out Of 25 As A Percent
Arias News
May 08, 2025 · 5 min read
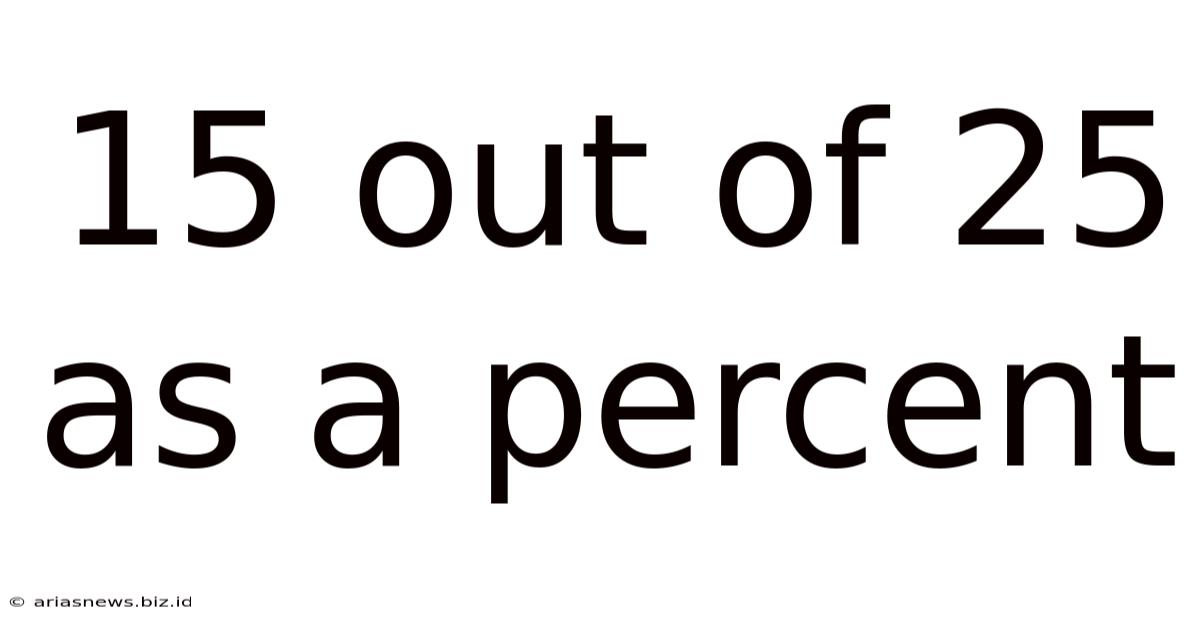
Table of Contents
15 out of 25 as a Percent: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications, from everyday budgeting and shopping to complex scientific analyses and financial modeling. Understanding how to convert fractions into percentages is crucial for anyone aiming to improve their numerical literacy and problem-solving abilities. This comprehensive guide delves into the method of calculating "15 out of 25 as a percent," providing a step-by-step explanation, practical examples, and exploring related percentage concepts.
Understanding Percentages
A percentage represents a fraction of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Calculating "15 out of 25" as a Percentage
The phrase "15 out of 25" represents a fraction: 15/25. To convert this fraction into a percentage, we need to express it as a fraction with a denominator of 100. Here's how we do it:
Step-by-Step Calculation:
-
Express the Fraction: Write the given information as a fraction: 15/25.
-
Find an Equivalent Fraction with a Denominator of 100: To achieve this, we need to find a number that, when multiplied by 25, equals 100. That number is 4 (25 x 4 = 100).
-
Multiply Both Numerator and Denominator: To maintain the value of the fraction, we must multiply both the numerator and the denominator by the same number (4 in this case).
(15 x 4) / (25 x 4) = 60/100
-
Express as a Percentage: A fraction with a denominator of 100 directly represents the percentage. Therefore, 60/100 is equal to 60%.
Therefore, 15 out of 25 is 60%.
Alternative Calculation Method: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first, then multiplying by 100 to obtain the percentage.
-
Convert the Fraction to a Decimal: Divide the numerator (15) by the denominator (25): 15 ÷ 25 = 0.6
-
Multiply by 100: Multiply the decimal by 100 to convert it to a percentage: 0.6 x 100 = 60%
This method yields the same result: 15 out of 25 is 60%.
Practical Applications of Percentage Calculations
Understanding percentage calculations has numerous practical applications in various aspects of life:
1. Academic Performance:
Calculating grades, understanding test scores, and assessing overall academic progress frequently involve percentage calculations. For example, if a student answers 15 questions correctly out of a total of 25, their score is 60%.
2. Financial Management:
Percentages are crucial for budgeting, calculating interest rates, understanding discounts, analyzing investment returns, and comprehending tax rates. For example, a 60% discount on a $100 item means a reduction of $60.
3. Sales and Marketing:
Businesses use percentages to track sales figures, calculate profit margins, analyze market share, and determine the effectiveness of marketing campaigns. A 60% increase in sales, for instance, indicates significant growth.
4. Scientific Research and Data Analysis:
Scientists and researchers extensively use percentages to represent data proportions, statistical significance, and error margins in studies and experiments.
5. Everyday Life:
Calculating tips in restaurants, understanding discounts in stores, and figuring out sales tax all require basic percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating "15 out of 25 as a percent" is straightforward, many percentage problems require more advanced techniques. Let's explore some examples:
1. Finding the Percentage Increase or Decrease:
Suppose a value increases from 20 to 30. To calculate the percentage increase:
- Find the difference: 30 - 20 = 10
- Divide the difference by the original value: 10 ÷ 20 = 0.5
- Multiply by 100: 0.5 x 100 = 50%
Therefore, there's a 50% increase.
Similarly, a decrease from 30 to 20 would result in a 33.33% decrease (calculated as (10 ÷ 30) x 100).
2. Finding a Percentage of a Number:
To find 60% of 200, multiply 200 by 0.6 (the decimal equivalent of 60%): 200 x 0.6 = 120.
3. Finding the Original Value after a Percentage Change:
If a value increased by 20% to become 120, to find the original value:
- Express the percentage as a decimal: 20% = 0.2
- Add 1 to the decimal: 1 + 0.2 = 1.2
- Divide the final value by the sum: 120 ÷ 1.2 = 100
Therefore, the original value was 100.
Mastering Percentages: Tips and Practice
Mastering percentage calculations requires consistent practice. Here are some tips:
-
Practice Regularly: Solve various percentage problems regularly to build your confidence and improve your speed.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages and fractions.
-
Use Multiple Methods: Try different approaches to solve the same problem, which helps in understanding the concepts more thoroughly.
-
Use Online Resources: Several online resources, including calculators and interactive exercises, can aid in your learning.
-
Apply Percentages to Real-Life Scenarios: Try calculating percentages in everyday situations, such as shopping discounts or calculating tips.
-
Check Your Work: Always double-check your answers to ensure accuracy.
By consistently applying these techniques and practicing diverse percentage problems, you can confidently tackle any percentage calculation, improving your numerical skills and problem-solving abilities in various academic, professional, and personal contexts. Remember that the foundation of percentage calculation lies in understanding fractions and their relationship to the number 100. With practice and understanding, mastering percentages becomes a readily applicable skill.
Latest Posts
Latest Posts
-
What Percentage Is 48 Out Of 50
May 08, 2025
-
How Much Is 900 000 In Pennies
May 08, 2025
-
Greatest Common Factor Of 63 And 42
May 08, 2025
-
2000 Is 10 Times As Much As
May 08, 2025
-
How Many Gallons Is 1 Inch Of Rain Per Acre
May 08, 2025
Related Post
Thank you for visiting our website which covers about 15 Out Of 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.