18 Is 30 Percent Of What Number
Arias News
May 12, 2025 · 4 min read
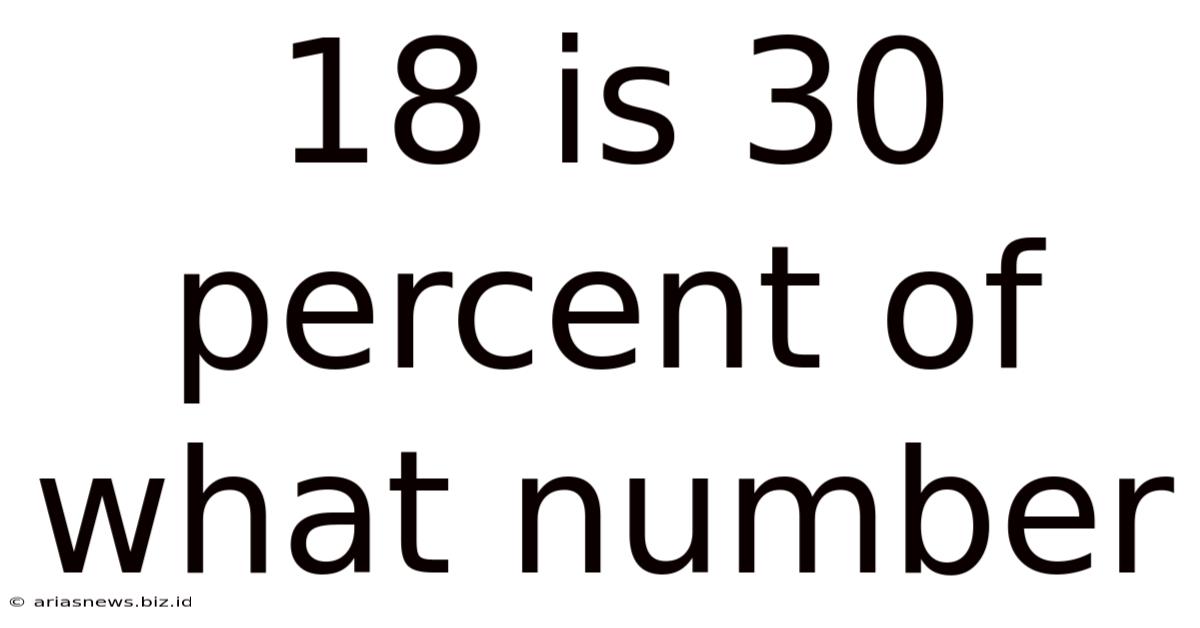
Table of Contents
18 is 30 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. This comprehensive guide delves into the question, "18 is 30 percent of what number?" We will explore different methods for solving this type of problem, offering clear explanations and practical examples to solidify your understanding of percentage calculations. We'll also touch upon the broader context of percentage problems and how these calculations are essential in various real-world scenarios.
Understanding Percentages
Before diving into the solution, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "18 is 30 percent of what number?" involves using the basic percentage formula:
Part = Percentage × Whole
In this equation:
- Part: Represents the portion of the whole that we know (in this case, 18).
- Percentage: Represents the percentage given (30%, or 0.30 as a decimal).
- Whole: Represents the total value we need to find.
Let's substitute the known values into the formula:
18 = 0.30 × Whole
To solve for the "Whole," we need to isolate it by dividing both sides of the equation by 0.30:
Whole = 18 / 0.30
Whole = 60
Therefore, 18 is 30 percent of 60.
Method 2: Setting up a Proportion
Another effective way to approach this problem is by setting up a proportion. A proportion shows the equality of two ratios. We can set up a proportion as follows:
18/x = 30/100
Where:
- 18 represents the part.
- x represents the unknown whole.
- 30 represents the percentage.
- 100 represents the total percentage (100%).
To solve for 'x', we cross-multiply:
18 * 100 = 30 * x
1800 = 30x
Now, divide both sides by 30:
x = 1800 / 30
x = 60
Again, we arrive at the same solution: 18 is 30 percent of 60.
Method 3: Using the Decimal Equivalent
We can also solve this problem by converting the percentage to its decimal equivalent and then setting up a simple equation. 30% is equivalent to 0.30 (obtained by dividing 30 by 100). So, the equation becomes:
18 = 0.30 * x
Dividing both sides by 0.30:
x = 18 / 0.30
x = 60
This method reaffirms our previous results: 18 is 30 percent of 60.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial for numerous real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, profit margins, and tax amounts all involve percentage calculations. For example, if a bank offers a 5% interest rate on savings, understanding percentages allows you to calculate the exact amount of interest you'll earn.
-
Shopping: Discounts are often expressed as percentages. Calculating the final price after a discount requires understanding percentage reductions. For example, a 20% discount on a $100 item can be easily calculated using percentage methods.
-
Data Analysis: Percentages are frequently used to represent data in graphs, charts, and reports. For instance, understanding the percentage of market share held by different companies provides valuable insights in business.
-
Science: Percentages are used to express concentrations of solutions or the efficiency of processes.
-
Everyday Life: Percentage calculations are used in tipping, calculating sales tax, determining nutritional information from food labels, and much more.
Expanding Your Percentage Skills: Further Examples
Let's explore a few more examples to solidify your understanding of percentage calculations:
Example 1: What is 25% of 80?
Using the formula: Part = Percentage × Whole
Part = 0.25 × 80 = 20
Example 2: 15 is what percent of 60?
Using the formula, and solving for the percentage:
Percentage = Part / Whole × 100
Percentage = 15 / 60 × 100 = 25%
Example 3: 30 is 12% of what number?
Using the formula, and solving for the whole:
Whole = Part / Percentage
Whole = 30 / 0.12 = 250
Troubleshooting Common Percentage Problems
When working with percentages, it's easy to make mistakes. Here are some common errors to watch out for:
-
Decimal Errors: Ensure you correctly convert percentages to decimals before performing calculations. A simple mistake here can drastically affect your result.
-
Formula Confusion: Make sure you're using the correct percentage formula for the specific problem you are trying to solve.
-
Incorrect Interpretation: Carefully read the problem to understand what is being asked. Misinterpreting the question will lead to incorrect answers.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable life skill. By understanding the fundamental concepts and formulas, you can confidently tackle various percentage-related problems. Whether it's calculating discounts, interest rates, or interpreting data, a solid grasp of percentages will empower you to make informed decisions in your personal and professional life. Remember to practice regularly, using a variety of problems to build your skills and confidence. The more you practice, the more proficient you will become at solving percentage problems efficiently and accurately. This comprehensive guide provides a strong foundation for success in tackling percentage calculations and offers solutions for common challenges encountered along the way. Continuous practice and careful attention to detail will ensure mastery of this essential mathematical skill.
Latest Posts
Latest Posts
-
How Much Is 160 Ml In Cups
May 12, 2025
-
How Do You Spell Juice In Spanish
May 12, 2025
-
How Many Quarts Are In 14 Cups
May 12, 2025
-
Can You Use California King Sheets On King Bed
May 12, 2025
-
Which Of These Techniques Involves An Intense Use Of Chiaroscuro
May 12, 2025
Related Post
Thank you for visiting our website which covers about 18 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.