2.3 Rounded To The Nearest Whole Number
Arias News
Mar 28, 2025 · 5 min read
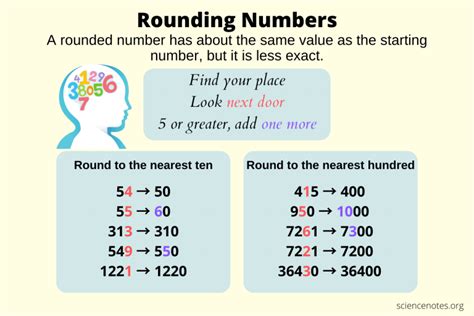
Table of Contents
2.3 Rounded to the Nearest Whole Number: A Comprehensive Guide
Rounding numbers is a fundamental concept in mathematics with widespread applications in various fields, from everyday calculations to complex scientific computations. Understanding how to round numbers accurately is crucial for ensuring precision and clarity in numerical representations. This comprehensive guide delves into the process of rounding 2.3 to the nearest whole number, exploring the underlying principles and practical implications. We'll also explore the broader context of rounding, including different rounding methods and their applications.
Understanding Rounding: The Basics
Rounding involves approximating a number to a specified level of precision. This precision is usually determined by the number of significant figures or decimal places required. The fundamental principle is to replace a number with a nearby value that is simpler or more manageable. In the context of rounding to the nearest whole number, we are aiming to find the closest integer to the given number.
The Rule of Rounding
The core rule for rounding is simple:
- If the digit to the right of the rounding place is 5 or greater, round up.
- If the digit to the right of the rounding place is less than 5, round down.
Let's break this down further:
- Rounding up: This means increasing the digit in the rounding place by one.
- Rounding down: This means keeping the digit in the rounding place the same.
Rounding 2.3 to the Nearest Whole Number
Applying the rule to our specific example, 2.3:
-
Identify the rounding place: In this case, we are rounding to the nearest whole number. The rounding place is the ones place (the digit to the left of the decimal point).
-
Look at the digit to the right of the rounding place: The digit to the right of the ones place is 3.
-
Apply the rule: Since 3 is less than 5, we round down. This means the digit in the ones place (2) remains unchanged.
-
The result: Therefore, 2.3 rounded to the nearest whole number is 2.
Visualizing the Process
Imagine a number line:
0 1 2 3 4 5 6
| | | | | | |
2.3 lies between 2 and 3. It's closer to 2 than to 3. This visual representation reinforces the logic of rounding 2.3 down to 2.
Significance and Applications
The seemingly simple act of rounding has profound implications across various disciplines:
-
Financial Calculations: Rounding is essential in financial reporting, ensuring that monetary values are presented in a clear and concise manner. For instance, rounding to the nearest cent or dollar is standard practice.
-
Scientific Measurements: In scientific experiments, rounding is used to report measurements to a specified level of accuracy. This prevents the propagation of errors and ensures consistency in data representation.
-
Statistical Analysis: Rounding plays a critical role in statistical analysis, simplifying large datasets and making calculations more manageable.
-
Engineering and Design: In engineering and design, rounding is vital for ensuring that dimensions and specifications are practical and easily implemented.
-
Everyday Life: We round numbers unconsciously in our daily lives, whether it's estimating the cost of groceries or determining travel time.
Different Rounding Methods
While the basic method discussed above is widely used, other rounding methods exist:
-
Rounding up: Always round the number up, regardless of the digit to the right of the rounding place. This is sometimes used in situations where error on the high side is preferred (e.g., ordering extra supplies to avoid shortages).
-
Rounding down: Always round the number down, regardless of the digit to the right of the rounding place. This is used when underestimation is more acceptable.
-
Rounding to the nearest even (Banker's Rounding): This method is designed to mitigate bias when rounding a large number of values. If the digit to the right of the rounding place is 5, the number is rounded to the nearest even number. For example, 2.5 would round to 2, while 3.5 would round to 4. This method is used in financial applications to minimize cumulative rounding errors.
-
Rounding to significant figures: This involves expressing a number to a specified number of significant digits. This is particularly important when dealing with scientific measurements or calculations where precision is paramount.
Advanced Considerations
-
Error Analysis: Understanding the potential error introduced by rounding is crucial, especially in scientific and engineering contexts. The error can accumulate with repeated rounding operations.
-
Programming and Algorithms: Many programming languages and algorithms incorporate rounding functions, providing options for different rounding methods.
-
Data Visualization: Rounding plays a significant role in data visualization, simplifying the presentation of large datasets while maintaining essential information.
Conclusion
Rounding 2.3 to the nearest whole number results in 2, a straightforward application of a fundamental mathematical concept. While seemingly simple, the act of rounding has profound implications across numerous fields, influencing accuracy, efficiency, and clarity in numerical representations. Understanding the various rounding methods and their applications is essential for anyone working with numbers, from students to professionals in diverse disciplines. By grasping the underlying principles and potential implications, one can effectively use rounding to simplify calculations, improve data analysis, and enhance the overall understanding of numerical information. The precision and accuracy achieved through proper rounding contribute significantly to the reliability and validity of various tasks and processes, highlighting its vital role in both practical and theoretical contexts. Therefore, mastering the art of rounding is not just about obtaining a correct answer; it's about understanding and managing the nuances of numerical representation and ensuring reliable results.
Latest Posts
Latest Posts
-
How Much Does 5 Gallons Of Concrete Weigh
Mar 31, 2025
-
What Is The Opposite Of An Inverse Relationship
Mar 31, 2025
-
5 Letter Word With Y As Second Letter
Mar 31, 2025
-
How Many Days Is 5 Million Seconds
Mar 31, 2025
-
What Do You Call A Female Bug That Floats
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 2.3 Rounded To The Nearest Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
