2 Times 10 To The Power Of 3
Arias News
May 12, 2025 · 5 min read
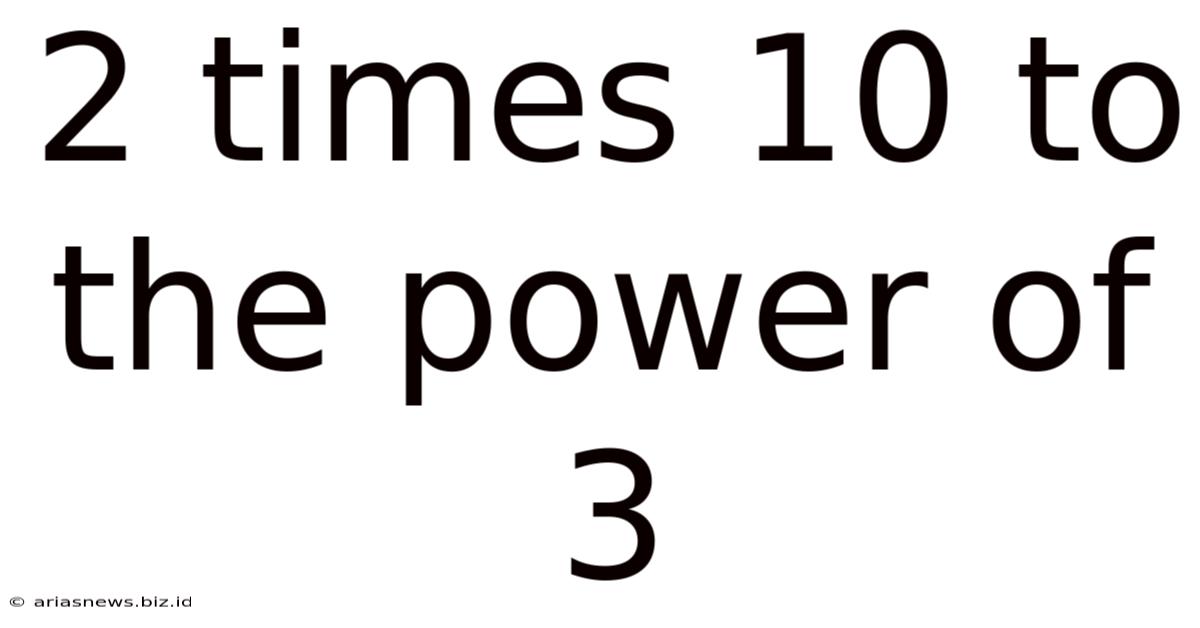
Table of Contents
Decoding 2 x 10³: Exploring Scientific Notation and its Applications
Scientific notation is a powerful tool used to represent extremely large or extremely small numbers concisely. Understanding this notation is crucial across various scientific fields, from astronomy to quantum physics. This article delves deep into the meaning and applications of 2 x 10³, a seemingly simple expression that unlocks a broader understanding of scientific notation and its significance in expressing quantities efficiently.
What Does 2 x 10³ Mean?
At its core, 2 x 10³ is a compact way of writing the number 2000. Let's break down its components:
-
10³: This represents 10 raised to the power of 3, which is calculated as 10 x 10 x 10 = 1000. The superscript '3' is called the exponent or power.
-
2 x 10³: This signifies multiplying 2 by 1000, resulting in 2000.
In essence, scientific notation expresses a number as a product of a coefficient (in this case, 2) and a power of 10. This format is particularly useful when dealing with numbers far removed from the range easily represented in standard decimal notation.
The Significance of Scientific Notation
The power of scientific notation lies in its ability to simplify the representation of both very large and very small numbers. Imagine trying to write out the number of atoms in a mole (approximately 6.022 x 10²³). Writing this out in standard form would be impractical and error-prone. Scientific notation provides a clear, concise, and easily understandable alternative.
Advantages of Scientific Notation:
- Conciseness: Represents large and small numbers efficiently, saving space and improving readability.
- Accuracy: Reduces the likelihood of errors in writing and interpreting lengthy numbers.
- Ease of Comparison: Makes comparing extremely large or small numbers easier.
- Computational Efficiency: Simplifies calculations involving multiplication and division of large or small numbers.
Applications of 2 x 10³ and Scientific Notation
While 2 x 10³ might seem like a relatively small number in the context of scientific notation, its representation highlights the fundamental principles applicable to numbers of vastly different magnitudes. Here are some examples showcasing the practical applications:
1. Measurement and Data Analysis
In various scientific disciplines, 2 x 10³ could represent a multitude of measurements. For instance:
- Physics: It could represent 2000 Joules of energy, 2000 meters of distance, or 2000 Hertz of frequency.
- Chemistry: It could represent the number of molecules in a specific sample or the volume of a solution in milliliters.
- Engineering: It could represent the weight of a component in grams, the voltage in a circuit, or the speed of a mechanism in rotations per minute.
The ability to represent these measurements concisely using scientific notation significantly enhances data analysis and interpretation.
2. Astronomy and Cosmology
Astronomy frequently employs scientific notation to handle immense distances and magnitudes. While 2 x 10³ is relatively small in this context, understanding its underlying principle extends to representing vast distances like the distance to nearby stars, the size of galaxies, or the age of the universe (approximately 13.8 x 10⁹ years).
3. Quantum Physics and Nanotechnology
At the opposite end of the scale, quantum physics and nanotechnology deal with extremely small quantities. While 2 x 10³ isn't in this realm, its underlying concept translates to representing the size of atoms, the wavelengths of light, or the mass of subatomic particles.
4. Computer Science and Data Storage
In the realm of data storage and processing, the concept of representing large numbers concisely is crucial. The amount of data stored in gigabytes (GB) or terabytes (TB) is often expressed using scientific notation to represent the capacity of hard drives or cloud storage systems. For instance, 2 terabytes could be represented as 2 x 10¹² bytes.
Expanding on Scientific Notation: Positive and Negative Exponents
Understanding 2 x 10³ lays a foundation for comprehending the broader application of scientific notation. The exponent determines the magnitude of the number:
-
Positive Exponents: Indicate large numbers; the higher the exponent, the larger the number. For example, 2 x 10⁶ (2,000,000) is larger than 2 x 10³.
-
Negative Exponents: Indicate small numbers (less than 1); the lower the exponent (i.e., more negative), the smaller the number. For example, 2 x 10⁻³ (0.002) is a small number.
Practical Exercises: Working with Scientific Notation
Let's solidify our understanding with a few examples:
Example 1: Convert 5,600,000 into scientific notation.
To do this, we move the decimal point to the left until we have a number between 1 and 10 (5.6). We moved the decimal point six places to the left, so the exponent is 6. Therefore, 5,600,000 in scientific notation is 5.6 x 10⁶.
Example 2: Convert 0.000045 into scientific notation.
Here, we move the decimal point to the right until we have a number between 1 and 10 (4.5). We moved the decimal point five places to the right, so the exponent is -5. Therefore, 0.000045 in scientific notation is 4.5 x 10⁻⁵.
Example 3: Perform the calculation: (2 x 10³) x (3 x 10⁴)
To multiply numbers in scientific notation, we multiply the coefficients (2 x 3 = 6) and add the exponents (3 + 4 = 7). Therefore, the answer is 6 x 10⁷.
Conclusion: The Enduring Relevance of Scientific Notation
2 x 10³, seemingly a straightforward expression, acts as a gateway to understanding the power and versatility of scientific notation. This concise method of representing numbers is essential across numerous scientific and technological disciplines, enabling efficient communication, computation, and analysis of quantities spanning an extraordinary range of magnitudes. Mastering this system is crucial for anyone seeking to navigate and understand the quantitative aspects of the world around us. The principles illustrated with this seemingly small number lay the groundwork for understanding the vastness of the cosmos and the intricacies of the quantum realm. It is a fundamental building block for scientific literacy and proficiency in quantitative fields.
Latest Posts
Latest Posts
-
Does Nathan And Haley Get A Divorce In Season 5
May 12, 2025
-
How Many Laps Is A 5000 M Race
May 12, 2025
-
What Is 0 472 Rounded To The Nearest Tenth
May 12, 2025
-
How Many Legs Do An Ant Have
May 12, 2025
-
Half A Yard Is How Many Inches
May 12, 2025
Related Post
Thank you for visiting our website which covers about 2 Times 10 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.