26 Out Of 30 Is What Percentage
Arias News
May 10, 2025 · 4 min read
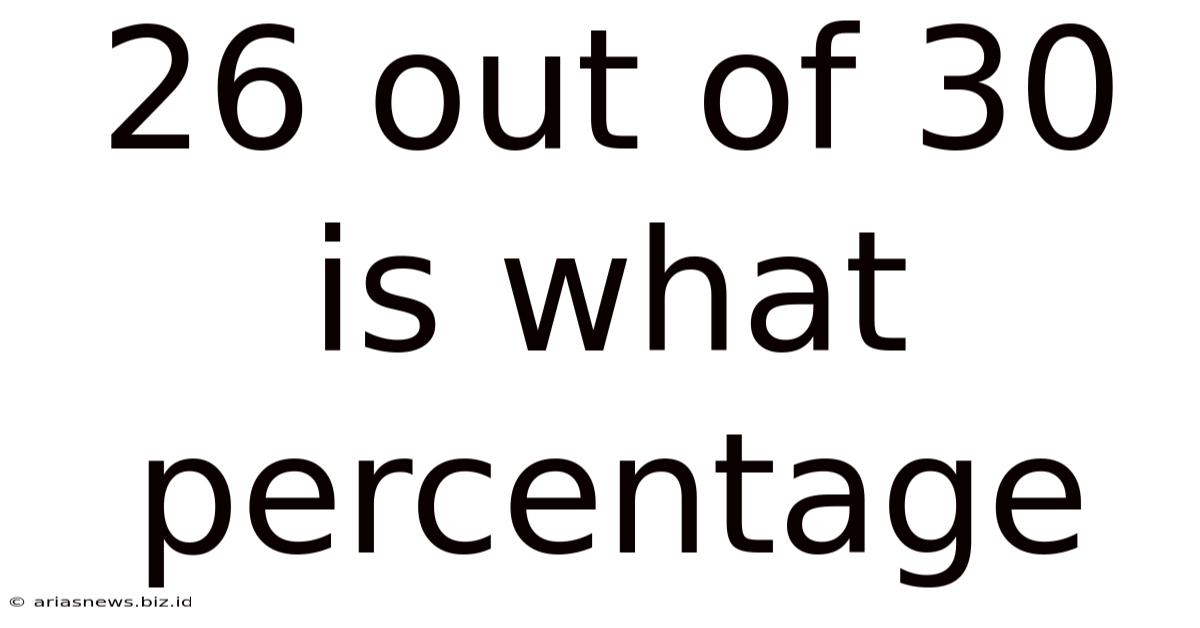
Table of Contents
26 out of 30 is What Percentage? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assignments and financial planning to everyday decision-making. Understanding how to determine percentages allows you to interpret data, make informed choices, and communicate numerical information effectively. This comprehensive guide will delve into the process of calculating the percentage that 26 out of 30 represents, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll also examine different methods of solving this type of problem and highlight potential pitfalls to avoid.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Percentages are a convenient way to represent proportions and make comparisons between different quantities.
Method 1: The Fraction Method
This is arguably the most straightforward approach. To find the percentage, we first express the given numbers as a fraction:
26/30
Next, we convert this fraction to a decimal by dividing the numerator (26) by the denominator (30):
26 ÷ 30 = 0.866666...
This decimal represents the proportion of 26 out of 30. To convert this decimal to a percentage, we multiply it by 100:
0.866666... × 100 ≈ 86.67%
Therefore, 26 out of 30 is approximately 86.67%. The use of the approximation symbol (≈) acknowledges the repeating decimal and the need for rounding.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion as follows:
26/30 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
30x = 2600
Then, we divide both sides by 30:
x = 2600/30 = 86.6666...
Again, converting this decimal to a percentage by multiplying by 100 gives us approximately 86.67%.
Method 3: The Percentage Formula
The percentage formula provides a more direct approach:
(Part/Whole) × 100 = Percentage
In our case:
(26/30) × 100 ≈ 86.67%
This formula directly reflects the core concept of percentages: the ratio of a part to the whole, expressed as a percentage.
Understanding the Result: 86.67%
The calculated percentage, 86.67%, signifies that 26 represents approximately 86.67% of 30. This value provides a concise and easily understandable representation of the proportion. This is useful in various contexts such as:
- Academic Performance: If a student answered 26 out of 30 questions correctly on a test, their score would be 86.67%.
- Sales Targets: If a salesperson achieved 26 out of 30 sales targets, their success rate would be 86.67%.
- Project Completion: If 26 out of 30 tasks in a project are completed, the project's completion rate is 86.67%.
Rounding and Precision
The result of 86.67% is a rounded value. The exact decimal value is a repeating decimal (0.86666...). The level of precision required depends on the context. For many applications, two decimal places (86.67%) are sufficient. However, in situations requiring higher accuracy, more decimal places might be necessary.
Common Mistakes to Avoid
- Incorrect Order of Operations: Ensure you divide the part (26) by the whole (30) before multiplying by 100.
- Forgetting to Multiply by 100: The final step of multiplying by 100 is crucial for converting the decimal to a percentage.
- Rounding Errors: While rounding is necessary, be mindful of the impact on accuracy. Clearly indicate rounded values using the approximation symbol (≈).
- Confusing Part and Whole: Always identify the "part" (the smaller number) and the "whole" (the larger number) correctly.
Advanced Applications: Working with Percentages
Understanding how to calculate percentages is a foundational skill that can be extended to more complex calculations:
- Percentage Increase/Decrease: Determining the percentage change between two values.
- Calculating Percentages of Percentages: Finding a percentage of an existing percentage.
- Compound Interest Calculations: Applying percentages iteratively over time.
- Statistical Analysis: Using percentages to interpret data and draw conclusions.
Conclusion: Mastering Percentage Calculations
The ability to accurately and efficiently calculate percentages is invaluable across a wide range of disciplines. This guide has demonstrated multiple methods for calculating the percentage that 26 out of 30 represents, highlighting the core principles and potential pitfalls. By understanding these methods and practicing regularly, you can confidently tackle percentage calculations in any context, enhancing your analytical skills and decision-making abilities. Remember to always clearly define the part and the whole, perform calculations accurately, and consider the appropriate level of precision when rounding your final answer. Mastering percentage calculations equips you with a powerful tool for interpreting data and solving problems in various fields.
Latest Posts
Latest Posts
-
What Two Words Added Together Contain The Most Letters
May 10, 2025
-
How Much Is 3 4 Cup Doubled
May 10, 2025
-
How Much Is 18 Ounces In Cups
May 10, 2025
-
How Many Pounds Are In 6 Tons
May 10, 2025
-
I Miss You My Buddy Smokey Robinson
May 10, 2025
Related Post
Thank you for visiting our website which covers about 26 Out Of 30 Is What Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.