3 4 Equals How Many Sixty Fourths
Arias News
May 11, 2025 · 5 min read
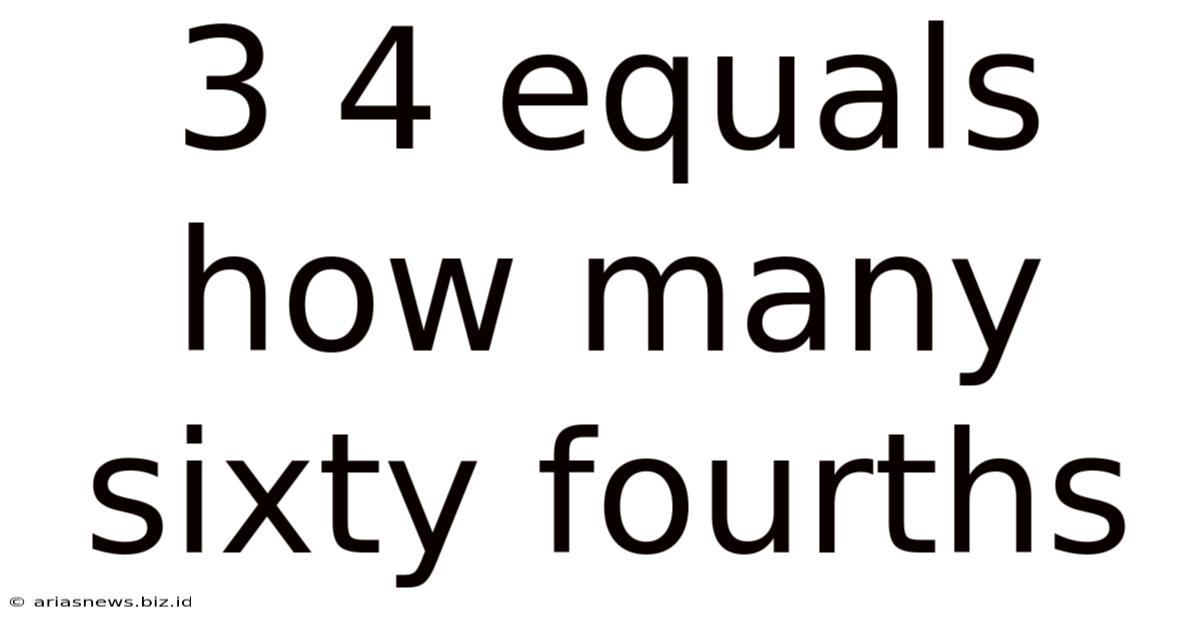
Table of Contents
3/4 Equals How Many Sixty-Fourths? A Deep Dive into Fractions
Understanding fractions is a cornerstone of mathematics, crucial for everything from baking a cake to complex engineering calculations. This article delves into the seemingly simple question: "3/4 equals how many sixty-fourths?" We'll explore the process of converting fractions, the underlying mathematical principles, and even touch upon practical applications to solidify your understanding. We will also cover various related concepts to expand your knowledge base and improve your overall fractional comprehension.
Understanding Fractions: A Quick Refresher
Before we tackle the conversion, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
Converting Fractions: The Core Principle
Converting fractions involves changing the denominator without altering the fraction's value. This is achieved by multiplying both the numerator and the denominator by the same number. This process maintains the ratio between the numerator and the denominator, ensuring the fractional value remains constant.
In our case, we need to convert 3/4 to an equivalent fraction with a denominator of 64. To achieve this, we ask ourselves: "What number multiplied by 4 equals 64?" The answer is 16 (4 x 16 = 64).
Therefore, we must multiply both the numerator and the denominator of 3/4 by 16:
(3 x 16) / (4 x 16) = 48/64
Therefore, 3/4 equals 48/64.
Visualizing the Conversion
Imagine a square divided into four equal parts. Shading three of these parts represents 3/4. Now, imagine dividing each of those four parts into 16 smaller, equal squares. You'll now have a total of 64 small squares (4 x 16 = 64). Notice that the shaded area, which previously represented 3/4, now occupies 48 of the 64 smaller squares (3 x 16 = 48). This visual representation helps solidify the concept of equivalent fractions.
Equivalent Fractions: A Deeper Look
The conversion of 3/4 to 48/64 illustrates the concept of equivalent fractions. Equivalent fractions represent the same value, even though they have different numerators and denominators. They are essentially different ways of expressing the same proportion or part of a whole.
Numerous equivalent fractions exist for any given fraction. For instance, 3/4 is also equivalent to 6/8, 9/12, 12/16, and so on. All these fractions represent the same proportion – three-quarters or 75%. The choice of which equivalent fraction to use often depends on the context of the problem or the desired level of precision.
Finding Equivalent Fractions: A Systematic Approach
To find equivalent fractions, simply multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio remains constant, thus preserving the fraction's value.
Practical Applications of Fraction Conversion
The ability to convert fractions is essential in various real-world applications, including:
-
Baking and Cooking: Recipes often require precise measurements, and converting fractions to a common denominator ensures accurate ingredient proportions. For instance, if a recipe calls for 3/4 cup of sugar and you have a 1/64 cup measuring spoon, converting 3/4 to sixty-fourths becomes crucial for precise measuring.
-
Construction and Engineering: Precise measurements are vital in construction and engineering projects. Converting fractions to a common denominator allows for accurate calculations and ensures the project's structural integrity.
-
Finance: Working with percentages and proportions in finance necessitates a strong understanding of fraction conversion. Converting fractions to a common denominator simplifies calculations involving interest rates, investments, and financial ratios.
-
Data Analysis: In data analysis, often you deal with proportions and percentages represented as fractions. Converting fractions to a common denominator allows for easy comparison and analysis of different datasets.
Beyond Sixty-Fourths: Expanding the Concept
While this article focuses on converting 3/4 to sixty-fourths, the principle extends to any denominator. To convert 3/4 to any other denominator (let's say 'x'), you simply need to find the number that, when multiplied by 4, equals 'x'. Then, multiply both the numerator and the denominator of 3/4 by that number.
Simplifying Fractions: The Inverse Process
The opposite of converting fractions to a larger denominator is simplifying fractions to a smaller denominator. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. Simplifying fractions reduces them to their lowest terms, making them easier to work with and understand.
Troubleshooting Common Mistakes
Several common mistakes can occur when converting fractions:
-
Only multiplying the numerator or denominator: Remember to always multiply both the numerator and the denominator by the same number.
-
Incorrect multiplication: Double-check your multiplication to ensure accuracy.
-
Forgetting to simplify: After converting, simplify the fraction to its lowest terms if possible.
Conclusion: Mastering Fraction Conversion
Mastering fraction conversion is a vital skill in mathematics and numerous real-world applications. Understanding the underlying principles – maintaining the ratio between numerator and denominator by multiplying or dividing both by the same number – is key. By practicing regularly and understanding the practical implications, you can confidently navigate the world of fractions and their conversions. Remember to visualize the process and check your work meticulously to avoid common pitfalls. The seemingly simple conversion of 3/4 to 48/64 serves as a gateway to a deeper understanding of fractions and their applications in various fields.
Latest Posts
Latest Posts
-
How Did Farmers Alliances Change The Way Small Farmers Operated
May 12, 2025
-
John Quincy Adams Coin 1825 To 1829 Worth
May 12, 2025
-
What Grade Is A 46 Out Of 50
May 12, 2025
-
Distance From Plano Tx To Dallas Tx
May 12, 2025
-
De Donde Es La Lada 951 En Usa
May 12, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Equals How Many Sixty Fourths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.