3 To The Power Of Negative 3
Arias News
Mar 28, 2025 · 5 min read
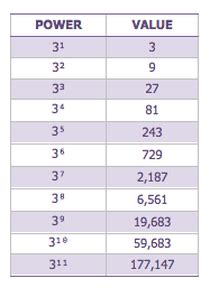
Table of Contents
Decoding 3 to the Power of Negative 3: A Deep Dive into Negative Exponents
Understanding exponents is fundamental to mathematics, and negative exponents, in particular, often present a stumbling block for many. This comprehensive guide will demystify the concept of 3 to the power of negative 3 (3⁻³), exploring its calculation, practical applications, and broader implications within the realm of algebra and beyond. We'll go beyond a simple numerical answer, delving into the underlying principles and showing you how to confidently tackle similar problems.
Understanding Exponents: A Quick Refresher
Before diving into negative exponents, let's revisit the basics. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example:
- 3² (3 to the power of 2 or 3 squared): This means 3 multiplied by itself twice: 3 * 3 = 9
- 3³ (3 cubed or 3 to the power of 3): This signifies 3 multiplied by itself three times: 3 * 3 * 3 = 27
- 3⁴ (3 to the power of 4): This represents 3 multiplied by itself four times: 3 * 3 * 3 * 3 = 81
You can see a clear pattern here: the exponent determines the number of times the base is used as a factor in the multiplication.
Introducing Negative Exponents
Now, let's introduce the concept of a negative exponent. A negative exponent doesn't indicate a negative number; instead, it signifies the reciprocal of the base raised to the positive exponent. In simpler terms, it flips the base number into a fraction.
The Rule: a⁻ⁿ = 1/aⁿ
Let's apply this rule to our specific example: 3⁻³
Calculating 3 to the Power of Negative 3
Using the rule for negative exponents, we can rewrite 3⁻³ as:
3⁻³ = 1/3³
Now, we calculate 3³ (3 to the power of 3), which we already know is 27.
Therefore:
3⁻³ = 1/27
So, 3 to the power of negative 3 equals 1/27.
Visualizing Negative Exponents: A Geometrical Perspective
It can be helpful to visualize exponents, especially negative ones. Imagine a cube with sides of length 3.
- 3³: Represents the volume of this cube (3 * 3 * 3 = 27 cubic units).
- 3⁻³: Can be thought of as the inverse volume, or how many such cubes would fit into a unit cube (a cube with sides of length 1). The answer, as we've calculated, is 1/27. This means 27 cubes with sides of length 3 would be needed to fill a unit cube.
This geometrical interpretation provides an intuitive understanding of what a negative exponent signifies—a reversal or inverse relationship.
Practical Applications of Negative Exponents
Negative exponents are not just abstract mathematical concepts; they find extensive applications in various fields:
1. Scientific Notation:
Scientific notation uses powers of 10 to represent very large or very small numbers. Negative exponents are crucial for expressing incredibly small numbers, such as the size of atoms or the mass of subatomic particles. For instance, 10⁻⁶ represents one millionth (0.000001).
2. Physics and Engineering:
Negative exponents frequently appear in physics and engineering formulas. For instance, inverse square laws, such as the inverse square law of gravity and Coulomb's law for electrostatics, utilize negative exponents to describe how forces weaken with distance.
3. Chemistry and Biology:
In chemistry, negative exponents are used to represent molar concentrations, particularly in dilute solutions. In biology, they can describe exponential decay processes, such as the decay of radioactive isotopes.
4. Finance and Economics:
Negative exponents are used in calculations involving compound interest, present value calculations, and other time-value-of-money concepts. The rate of discount is often expressed with a negative exponent.
5. Computer Science:
In computer science, negative exponents are used in calculations involving data sizes, memory management, and algorithm analysis, particularly when dealing with very large or very small datasets.
Expanding the Concept: Rules of Exponents
Understanding the calculation of 3⁻³ is only part of the puzzle. Mastery of exponents requires familiarity with their rules:
- Product Rule: aᵐ * aⁿ = aᵐ⁺ⁿ (when multiplying bases with the same exponent, add the exponents)
- Quotient Rule: aᵐ / aⁿ = aᵐ⁻ⁿ (when dividing bases with the same exponent, subtract the exponents)
- Power Rule: (aᵐ)ⁿ = aᵐⁿ (when raising a power to another power, multiply the exponents)
- Zero Exponent Rule: a⁰ = 1 (any non-zero base raised to the power of zero equals 1)
- Negative Exponent Rule: a⁻ⁿ = 1/aⁿ (as already discussed)
These rules are interconnected and crucial for simplifying complex expressions involving exponents, both positive and negative.
Solving More Complex Problems with Negative Exponents
Let's consider a slightly more complex problem to illustrate the application of these rules:
Simplify (3⁻² * 3⁴) / 3⁻¹
- Apply the product rule to the numerator: 3⁻² * 3⁴ = 3⁻²⁺⁴ = 3² = 9
- Rewrite the expression: 9 / 3⁻¹
- Apply the negative exponent rule to the denominator: 9 / (1/3) = 9 * 3 = 27
Therefore, (3⁻² * 3⁴) / 3⁻¹ simplifies to 27.
This example shows how the rules of exponents work together to simplify expressions, even those containing negative exponents.
Beyond the Basics: Fractional and Decimal Exponents
The concept of exponents can be extended beyond integers to include fractions and decimals. A fractional exponent represents a root operation. For instance:
- a¹⁄² = √a (square root)
- a¹⁄³ = ³√a (cube root)
- aᵐ⁄ⁿ = ⁿ√aᵐ (nth root of a to the power m)
Decimal exponents can be handled by converting them to fractional exponents for simplification.
Troubleshooting Common Mistakes
When working with negative exponents, it's common to make certain mistakes. Here are some points to watch out for:
- Confusing negative exponents with negative numbers: A negative exponent does not mean the result is negative. It means the reciprocal of the base raised to the positive power.
- Incorrectly applying the rules of exponents: Carefully review and apply the product, quotient, and power rules for exponents.
- Forgetting to handle parentheses correctly: Parentheses significantly affect the order of operations. Ensure you carefully consider the order of operations while dealing with expressions that include exponents.
Conclusion: Mastering Negative Exponents
Understanding 3⁻³ and, more broadly, negative exponents is a crucial step in mastering algebra and its numerous applications. By applying the fundamental rules of exponents and grasping the underlying principles, you can confidently tackle complex mathematical problems. Remember, negative exponents represent a reciprocal relationship and are essential for expressing very small numbers and formulating various scientific and engineering concepts. Practice is key to developing proficiency, so continue to work through various examples to solidify your understanding. The ability to work confidently with negative exponents will significantly enhance your mathematical skills and open doors to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Many Feet Are In A City Block
Mar 31, 2025
-
How Many Slices Of Pizza In A 9 Inch
Mar 31, 2025
-
How Many Miles Is 10 Minutes Driving
Mar 31, 2025
-
Average Bench Press For 13 Year Old
Mar 31, 2025
-
How Many Ice Cubes In A Cup
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 3 To The Power Of Negative 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
