30 000 Is 20 Percent Of What
Arias News
Mar 30, 2025 · 5 min read
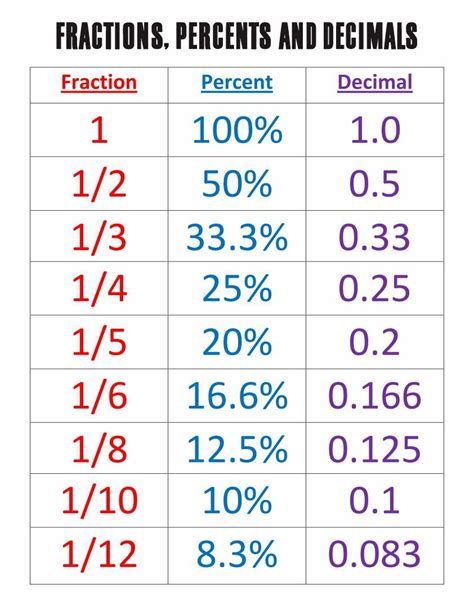
Table of Contents
30,000 is 20 Percent of What? A Comprehensive Guide to Percentage Calculations
Finding out what a certain percentage represents of a larger whole is a fundamental mathematical skill with broad applications across various fields. Whether you're dealing with budgeting, sales targets, investment returns, or even baking recipes, understanding percentage calculations is crucial. This article delves into how to determine the original number when you know a percentage of it, specifically tackling the question: 30,000 is 20 percent of what? We will not only solve this problem but also equip you with the tools and knowledge to tackle similar percentage problems independently.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction expressed as a number out of 100. For instance, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20. This representation is key to solving percentage problems.
The Formula: Unraveling the Mystery
The core formula we'll use to solve "30,000 is 20 percent of what?" is:
(Percentage/100) * Whole = Part
In our scenario:
- Part: This is the known value, which is 30,000.
- Percentage: This is also known, which is 20.
- Whole: This is the unknown value we need to find. Let's represent it with 'x'.
Substituting these values into the formula, we get:
(20/100) * x = 30,000
Solving the Equation: Step-by-Step Guide
Now, let's solve for 'x':
-
Simplify the fraction: 20/100 simplifies to 1/5. The equation becomes:
(1/5) * x = 30,000
-
Isolate 'x': To isolate 'x', we multiply both sides of the equation by 5:
5 * (1/5) * x = 30,000 * 5
-
Solve for x: This simplifies to:
x = 150,000
Therefore, 30,000 is 20 percent of 150,000.
Alternative Methods: Different Approaches, Same Result
While the above method is straightforward, let's explore alternative approaches to solving this type of percentage problem, showcasing the versatility of percentage calculations.
Method 2: Using Decimal Equivalents
Instead of using fractions, we can use decimal equivalents. 20% is equal to 0.20. The equation becomes:
0.20 * x = 30,000
To solve for x, divide both sides by 0.20:
x = 30,000 / 0.20
x = 150,000
This method yields the same result, demonstrating that different mathematical approaches can lead to the same accurate answer.
Method 3: The Proportion Method
The proportion method utilizes the concept of ratios. We can set up a proportion as follows:
20/100 = 30,000/x
Cross-multiply to solve for x:
20 * x = 100 * 30,000
20x = 3,000,000
x = 3,000,000 / 20
x = 150,000
Again, we arrive at the same solution, emphasizing the reliability and consistency of various mathematical techniques in percentage calculations.
Real-World Applications: Where Percentage Calculations Matter
Understanding percentage calculations isn't just about solving mathematical problems; it has far-reaching practical applications across numerous fields. Let's explore some examples:
- Finance: Calculating interest rates, investment returns, discounts, tax rates, and loan payments all rely heavily on percentage calculations. For example, if you receive a 10% return on a $5,000 investment, knowing how to calculate that percentage increase is essential for assessing your financial gains.
- Sales and Marketing: Determining sales targets, commission rates, profit margins, and market share all involve percentage calculations. If a company aims to increase sales by 15% in the next quarter, understanding percentage change is crucial for planning and strategy.
- Data Analysis: Percentages are fundamental in analyzing data sets, representing proportions, and visualizing trends. For example, if a survey shows that 75% of respondents prefer a particular product, that percentage is key to interpreting the survey results.
- Everyday Life: Percentage calculations are often encountered in daily life. Calculating tips at restaurants, figuring out discounts at sales, or understanding nutrition labels (e.g., percentage of daily value for nutrients) all involve percentage calculations.
- Science and Engineering: Percentages are ubiquitous in scientific and engineering fields, expressing concentrations, efficiencies, and error rates.
Beyond the Basics: Handling More Complex Scenarios
While this article focused on a specific problem ("30,000 is 20 percent of what?"), the principles can be extended to more complex scenarios. Here are some examples:
- Calculating percentage increase or decrease: This involves finding the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] * 100% - Finding the percentage of a number: This involves calculating a specific percentage of a given number (e.g., finding 15% of 250).
- Determining the original value after a percentage increase or decrease: This is similar to the problem we solved, but involves working backward from a value that has already been increased or decreased by a certain percentage.
Master the Art of Percentage Calculations: Tips and Tricks
To improve your proficiency in percentage calculations:
- Practice regularly: The more you practice, the more comfortable and efficient you'll become. Work through various examples and challenge yourself with different scenarios.
- Use different methods: Experiment with different methods (fractional, decimal, proportion) to find the approach that suits your thinking style best.
- Visual aids: Charts and diagrams can help visualize percentage relationships.
- Utilize online calculators: While understanding the underlying principles is crucial, online calculators can be helpful for double-checking your work or tackling more complex problems.
- Break down complex problems: Large or complex percentage problems can often be broken down into smaller, more manageable steps.
Conclusion: Empowering Yourself with Percentage Skills
Understanding percentage calculations is a valuable skill that extends beyond the realm of mathematics, impacting various aspects of life. By mastering this fundamental concept, you'll be better equipped to make informed decisions in finance, sales, data analysis, and countless other areas. Remember the core formula, explore various methods, and practice regularly to hone your skills. With consistent effort, you'll become confident in tackling percentage problems, regardless of their complexity. The ability to quickly and accurately calculate percentages will undoubtedly prove to be a valuable asset in both your personal and professional life.
Latest Posts
Latest Posts
-
How Much Does A Two Liter Weigh
Apr 01, 2025
-
How Much Does 100 In Quarters Weigh
Apr 01, 2025
-
How Long Will It Take To Walk 2 5 Miles
Apr 01, 2025
-
38 As A Fraction Of An Inch
Apr 01, 2025
-
How Many Cc Is In A Gram
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 30 000 Is 20 Percent Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
