33 Out Of 35 As A Percentage
Arias News
May 11, 2025 · 4 min read
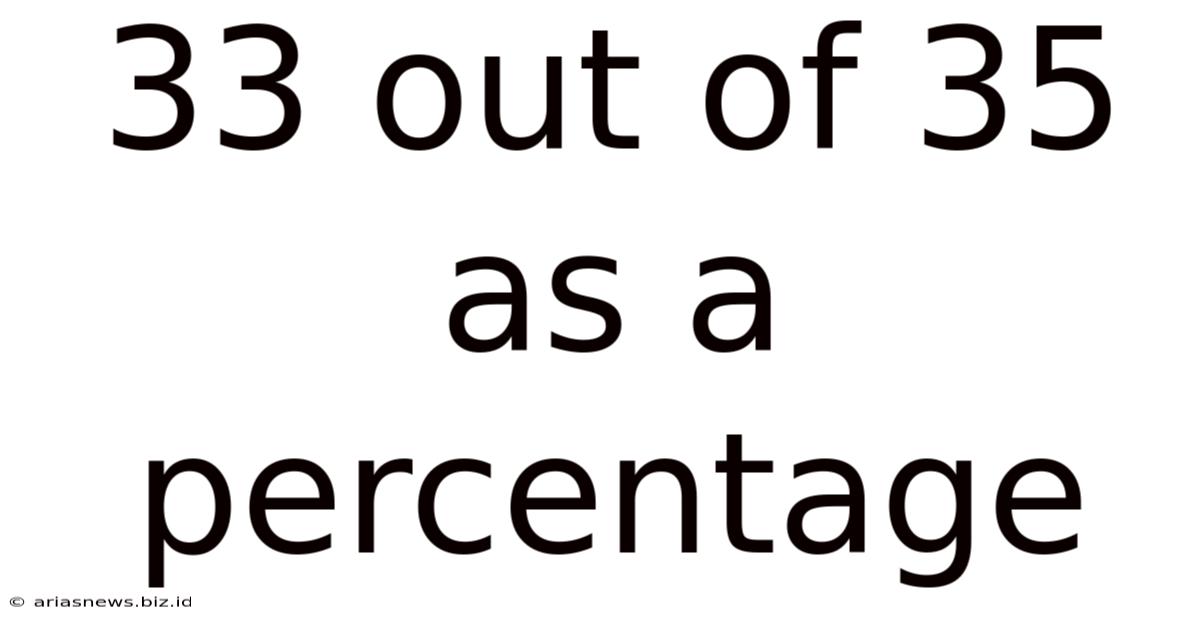
Table of Contents
33 out of 35 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to convert fractions into percentages is crucial for interpreting data and making informed decisions. This comprehensive guide will explore how to calculate 33 out of 35 as a percentage, along with various methods, practical applications, and related percentage calculations. We'll also delve into the concept of percentage error and its significance.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "out of 100." Percentages are used extensively to represent proportions, changes, and rates. For example, a score of 90% on a test means you answered 90 out of 100 questions correctly.
Calculating 33 out of 35 as a Percentage
There are several ways to calculate 33 out of 35 as a percentage. Let's explore the most common methods:
Method 1: Using the Fraction Method
This is the most straightforward method. We express the given numbers as a fraction and then convert the fraction to a percentage:
-
Express as a fraction: 33 out of 35 can be written as the fraction 33/35.
-
Convert to a decimal: Divide the numerator (33) by the denominator (35): 33 ÷ 35 ≈ 0.9429
-
Convert to a percentage: Multiply the decimal by 100: 0.9429 × 100 = 94.29%
Therefore, 33 out of 35 is approximately 94.29%.
Method 2: Using Proportions
This method uses the concept of proportions to solve for the percentage:
-
Set up a proportion: Let 'x' represent the percentage. We can set up the proportion: 33/35 = x/100
-
Cross-multiply: Multiply 33 by 100 and 35 by x: 3300 = 35x
-
Solve for x: Divide both sides by 35: x = 3300 ÷ 35 ≈ 94.29
Therefore, x ≈ 94.29%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply enter 33 ÷ 35 and then multiply by 100 to obtain the percentage.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations:
- Academic Performance: Calculating grades, assessing test scores, and determining overall performance.
- Finance: Calculating interest rates, discounts, taxes, profits, and losses.
- Statistics: Analyzing data, representing proportions, and interpreting survey results.
- Business: Tracking sales figures, calculating profit margins, and analyzing market share.
- Everyday Life: Determining tips, calculating discounts, and understanding sales promotions.
Related Percentage Calculations
Understanding how to calculate 33 out of 35 also allows you to easily calculate related percentages:
-
Percentage of error: This is crucial in scientific and engineering contexts. It represents the difference between an experimental value and a theoretical value, expressed as a percentage. A smaller percentage error signifies greater accuracy. We'll delve into this in more detail later.
-
Calculating the remaining percentage: If 33 out of 35 represent 94.29%, then the remaining percentage (representing the 2 out of 35) is 100% - 94.29% = 5.71%.
-
Scaling up or down: If a certain percentage applies to a sample of 35, we can easily scale that percentage to apply to larger or smaller samples using proportional reasoning.
Percentage Error: Understanding Accuracy
Percentage error is a crucial concept that helps us quantify the accuracy of measurements or calculations. It's particularly important in scientific experiments and engineering projects where precision is paramount.
The formula for percentage error is:
Percentage Error = [(|Experimental Value - Theoretical Value|) / Theoretical Value] × 100
Where:
- Experimental Value: The value obtained through measurement or experiment.
- Theoretical Value: The expected or true value.
- | | represents the absolute value (ignoring the negative sign).
Let's consider an example: Suppose the theoretical value of a measurement is 35, and the experimental value is 33. The percentage error would be:
Percentage Error = [(|33 - 35|) / 35] × 100 = (2 / 35) × 100 ≈ 5.71%
This indicates a 5.71% error in the measurement. A lower percentage error suggests a higher degree of accuracy.
Beyond the Basics: Advanced Percentage Applications
The ability to calculate percentages opens doors to more complex calculations and analyses. Here are a few examples:
-
Compound Interest: Calculating the total amount accumulated over time considering the interest earned on both the principal and the accumulated interest.
-
Percentage Change: Determining the relative change between two values (e.g., calculating the percentage increase or decrease in sales).
-
Weighted Averages: Calculating averages where different values have different weights or importance.
-
Statistical Significance: In statistical analysis, percentages play a crucial role in determining the significance of results and drawing inferences from data.
Conclusion: Mastering Percentages for Success
Mastering percentage calculations is a valuable skill applicable in a wide variety of contexts. From everyday transactions to complex scientific analyses, understanding how to calculate and interpret percentages is essential for informed decision-making. This guide has explored several methods for calculating 33 out of 35 as a percentage, alongside practical applications and related concepts like percentage error. By understanding these principles, you can effectively analyze data, solve problems, and make sound judgments in various aspects of your life and career. Remember, practice makes perfect, so continue honing your skills through various exercises and real-world applications. The more comfortable you are with percentage calculations, the more confident and successful you'll be in tackling numerous challenges that involve numerical analysis and interpretation.
Latest Posts
Latest Posts
-
How Many Words Can You Make From Halloween
May 12, 2025
-
How Many Weight Watchers Points Is Cheese
May 12, 2025
-
What Is 9 To The Power Of 9
May 12, 2025
-
Feliz Navidad Prospero Ano Y Felicidad In English
May 12, 2025
-
Water Temperature In A Three Compartment Sink
May 12, 2025
Related Post
Thank you for visiting our website which covers about 33 Out Of 35 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.