4 And 1 2 As A Decimal
Arias News
Mar 31, 2025 · 5 min read
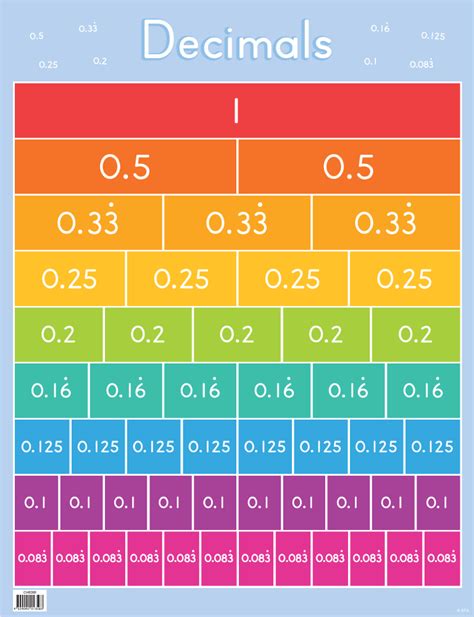
Table of Contents
4 and 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, with applications spanning various fields. This comprehensive guide delves into the conversion of the mixed number 4 and 1/2 into its decimal equivalent, exploring the process, its applications, and related concepts. We'll also touch upon the broader context of fraction-to-decimal conversions and their significance in the world of numbers.
Understanding Mixed Numbers and Decimals
Before we dive into the conversion, let's clarify the terms involved. A mixed number combines a whole number and a fraction, like 4 and 1/2. A decimal, on the other hand, represents a number using a base-ten system, with digits placed to the right of a decimal point representing tenths, hundredths, thousandths, and so on.
The core concept here is representing a portion of a whole. Fractions do this directly, while decimals offer another, equally valid, representation. Understanding both and how to convert between them is crucial for mathematical fluency.
Converting 4 and 1/2 to a Decimal: The Step-by-Step Process
There are several ways to convert 4 and 1/2 to a decimal. Let's explore the most common and straightforward methods:
Method 1: Converting the Fraction to a Decimal
This method involves focusing on the fractional part of the mixed number first. The fraction 1/2 represents one part out of two equal parts. To convert this to a decimal, we perform the division:
1 ÷ 2 = 0.5
This means that 1/2 is equivalent to 0.5. Now, we simply add the whole number:
4 + 0.5 = 4.5
Therefore, 4 and 1/2 as a decimal is 4.5.
Method 2: Converting the Mixed Number to an Improper Fraction
Another approach involves first converting the mixed number into an improper fraction. An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number).
To convert 4 and 1/2 to an improper fraction:
- Multiply the whole number (4) by the denominator of the fraction (2): 4 * 2 = 8
- Add the numerator of the fraction (1) to the result: 8 + 1 = 9
- Keep the same denominator (2): The improper fraction is 9/2.
Now, divide the numerator by the denominator:
9 ÷ 2 = 4.5
Again, we arrive at the decimal equivalent of 4.5.
Practical Applications of Decimal Representation
The decimal representation of 4 and 1/2, or 4.5, finds applications in numerous real-world scenarios:
-
Measurements: Imagine measuring the length of a piece of wood. If it's 4 and a half feet long, you'd likely record this as 4.5 feet. This is far more common and practical than using the mixed number form in most measurement contexts.
-
Finance: Dealing with monetary values often involves decimals. $4.50 represents four and a half dollars, a straightforward decimal representation readily understood in financial transactions.
-
Data Analysis: In statistical analysis and data presentation, decimals are essential for representing data points accurately and concisely.
-
Scientific Calculations: Many scientific calculations and measurements rely heavily on decimal representation for precision and ease of calculation.
-
Computer Programming: Computers primarily work with decimal representations of numbers, making the conversion essential in many programming tasks.
Beyond 4 and 1/2: Converting Other Fractions to Decimals
The methods described above can be applied to convert other fractions to decimals. The key principle remains the same: division of the numerator by the denominator.
Let's consider a few examples:
- 3/4: 3 ÷ 4 = 0.75
- 1/3: 1 ÷ 3 = 0.333... (a repeating decimal)
- 5/8: 5 ÷ 8 = 0.625
- 2 and 3/5: First, convert to an improper fraction (13/5), then divide: 13 ÷ 5 = 2.6
Repeating Decimals: It's important to note that some fractions, like 1/3, result in repeating decimals. These are indicated by placing a bar over the repeating digit(s), such as 0.3̅3̅3̅... This signifies that the digit 3 repeats infinitely.
Significance of Fraction-to-Decimal Conversion
The ability to convert between fractions and decimals is a cornerstone of mathematical literacy. It allows for flexibility in representing and manipulating numerical values. Understanding this conversion enhances problem-solving capabilities across a wide range of applications. It bridges the gap between different numerical representations, enabling seamless transitions between fractions, often used in theoretical calculations, and decimals, often preferred for practical and computational purposes.
For instance, in baking, a recipe might call for 1/2 cup of sugar. A baker might easily translate this to 0.5 cups for more precise measurement using a digital scale. Similarly, in engineering, understanding the conversion allows for accurate calculations and avoids potential errors arising from inconsistent numerical representations.
Advanced Concepts and Further Exploration
While the conversion of 4 and 1/2 to 4.5 is relatively straightforward, understanding the underlying principles allows for tackling more complex conversions. Here are some areas for further exploration:
-
Converting decimals to fractions: This is the reverse process, which involves identifying the place value of the decimal digits and expressing the number as a fraction.
-
Working with percentages: Percentages are essentially fractions expressed as parts per hundred (e.g., 50% is equivalent to 1/2 or 0.5). Understanding the relationship between fractions, decimals, and percentages is crucial.
-
Understanding different number systems: While this guide focuses on the decimal system (base 10), exploring other number systems, such as binary (base 2) or hexadecimal (base 16), provides a deeper understanding of numerical representations.
-
Using calculators and software: Calculators and software packages can greatly simplify the conversion process, particularly for more complex fractions. Understanding the underlying principles, however, remains vital for interpreting the results and avoiding errors.
Conclusion: Mastering the Conversion
The conversion of 4 and 1/2 to its decimal equivalent, 4.5, is a simple yet fundamental concept with far-reaching applications. Mastering this conversion enhances mathematical proficiency and opens doors to tackling more complex numerical problems. By understanding the underlying principles and exploring related concepts, you can develop a strong foundation in numerical literacy, enabling you to confidently navigate mathematical challenges in various aspects of life and professional endeavors. The ability to seamlessly move between fractions and decimals empowers you to solve problems more efficiently and accurately, ultimately contributing to success in fields ranging from everyday calculations to advanced scientific and engineering pursuits.
Latest Posts
Latest Posts
-
How Long Does It Take For Soda To Freeze
Apr 02, 2025
-
What Number Is 24 Percent Of 75
Apr 02, 2025
-
What Does Ya Ya Mean In Greek
Apr 02, 2025
-
Which Is Longer A Yard Or A Meter
Apr 02, 2025
-
How Many Minutes Are In 540 Seconds
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 4 And 1 2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
