40 Percent Of What Number Is 12
Arias News
May 09, 2025 · 5 min read
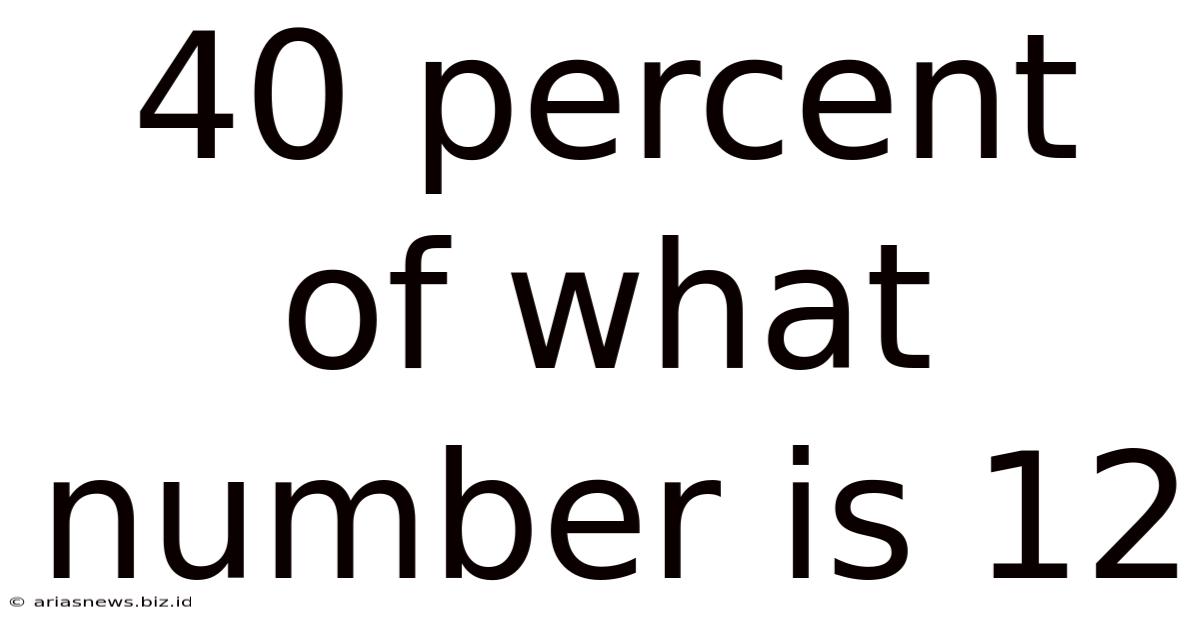
Table of Contents
40 Percent of What Number is 12? Unlocking the Power of Percentages
Finding the answer to "40 percent of what number is 12?" might seem like a simple math problem, but it unlocks a world of practical applications. Understanding percentages is fundamental to various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will not only provide the solution but also delve into the methods, practical examples, and the broader implications of percentage calculations.
Understanding Percentages: A Foundation
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage represents a fraction of 100. For instance, 40% means 40 out of 100, or 40/100, which simplifies to 2/5. This fractional representation is crucial for solving percentage problems.
Key Terminology
- Percentage: A fraction or ratio expressed as a number out of 100.
- Base Number: The whole number from which the percentage is calculated. This is the number we're trying to find in the question "40 percent of what number is 12?"
- Part: The portion of the base number represented by the percentage. In our problem, the part is 12.
- Rate: The percentage itself (40% in this case).
Solving "40 Percent of What Number is 12?"
There are several approaches to solve this problem. We'll explore two common methods: the algebraic method and the unitary method.
Method 1: The Algebraic Approach
This method utilizes algebraic equations to solve for the unknown base number.
-
Translate the problem into an equation: "40 percent of what number is 12" translates to:
0.40 * x = 12
Where 'x' represents the unknown number. We convert 40% to its decimal equivalent (0.40).
-
Solve for x: To isolate 'x', divide both sides of the equation by 0.40:
x = 12 / 0.40
-
Calculate the result:
x = 30
Therefore, 40% of 30 is 12.
Method 2: The Unitary Method
The unitary method focuses on finding the value of one unit (1%) before scaling it up to the required percentage.
-
Find the value of 1%: If 40% of a number is 12, then 1% of that number would be:
12 / 40 = 0.3
-
Find the value of 100%: Since 1% is 0.3, 100% (the whole number) would be:
0.3 * 100 = 30
Therefore, 40% of 30 is 12.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in a wide array of real-world scenarios:
1. Financial Matters:
- Discounts: Calculating discounts on sale items. For example, a 20% discount on a $100 item means a saving of $20, leaving a final price of $80.
- Taxes: Determining the amount of sales tax or income tax payable. A 6% sales tax on a $50 purchase would be $3.
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans. A 5% interest rate on a $1000 loan would mean $50 interest in one year (simple interest).
- Investment Returns: Analyzing investment performance. A 10% return on a $5000 investment would yield a profit of $500.
- Profit Margins: Calculating the profit margin of a business. A 15% profit margin on a product costing $20 would indicate a profit of $3.
2. Statistical Analysis:
- Data Representation: Percentages are used extensively to represent data in charts, graphs, and reports. For example, showing the percentage of respondents who prefer a particular product in a survey.
- Probability: Calculating the probability of events happening. A 70% chance of rain indicates a high likelihood of precipitation.
- Growth Rates: Measuring the growth rate of populations, economies, or businesses. A 5% annual growth rate signifies a steady increase.
3. Everyday Life:
- Tipping: Calculating tips in restaurants. A 15% tip on a $50 meal would be $7.50.
- Cooking: Adjusting recipes based on percentages. If a recipe calls for 20% less sugar, you would reduce the amount accordingly.
- Comparisons: Comparing different values using percentages. Comparing the performance of two different products using percentage change.
Advanced Percentage Problems and Solutions
Let's explore some more complex percentage scenarios to further enhance your understanding:
Problem 1: Finding the Percentage Increase or Decrease
Suppose the price of a product increased from $50 to $60. What is the percentage increase?
- Calculate the difference: $60 - $50 = $10
- Calculate the percentage increase: ($10 / $50) * 100% = 20%
The price increased by 20%.
Problem 2: Successive Percentages
If a product is discounted by 20% and then another 10% is applied, what is the total discount?
This isn't simply adding the percentages. We need to calculate sequentially.
- First discount: 20% discount on the original price reduces the price to 80% of the original.
- Second discount: A further 10% discount on the reduced price (80%) means we're paying 90% of the 80%. This equates to 0.90 * 0.80 = 0.72.
- Total discount: The final price is 72% of the original, so the total discount is 100% - 72% = 28%.
Therefore, the total discount is 28%.
Problem 3: Finding the Original Price After a Percentage Increase
The price of an item increased by 15% to become $75. What was the original price?
- Represent the original price: Let's denote the original price as 'x'.
- Set up the equation: The new price is 115% of the original price (100% + 15%), so: 1.15 * x = 75
- Solve for x: x = 75 / 1.15 = $65.22 (approximately)
The original price was approximately $65.22.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a crucial life skill. From managing finances to interpreting data, the ability to perform percentage calculations efficiently and accurately is invaluable. While the simple problem of "40 percent of what number is 12?" might seem basic, it serves as a gateway to mastering a wider range of percentage-based problems. By understanding the underlying principles and practicing different methods, you can confidently tackle various percentage-related challenges encountered in daily life and professional endeavors. Remember to practice consistently, and you'll soon find yourself adept at solving even the most complex percentage problems with ease and precision.
Latest Posts
Latest Posts
-
Which Best Describes A Difference Between Transcription And Dna Replication
May 09, 2025
-
How Big Is 50 Acres In Miles
May 09, 2025
-
What Is The Closest Ocean To Me
May 09, 2025
-
How Many Servings Are In A Gallon
May 09, 2025
-
6875 As A Fraction In Simplest Form
May 09, 2025
Related Post
Thank you for visiting our website which covers about 40 Percent Of What Number Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.