40 Percent Of What Number Is 20
Arias News
May 09, 2025 · 5 min read
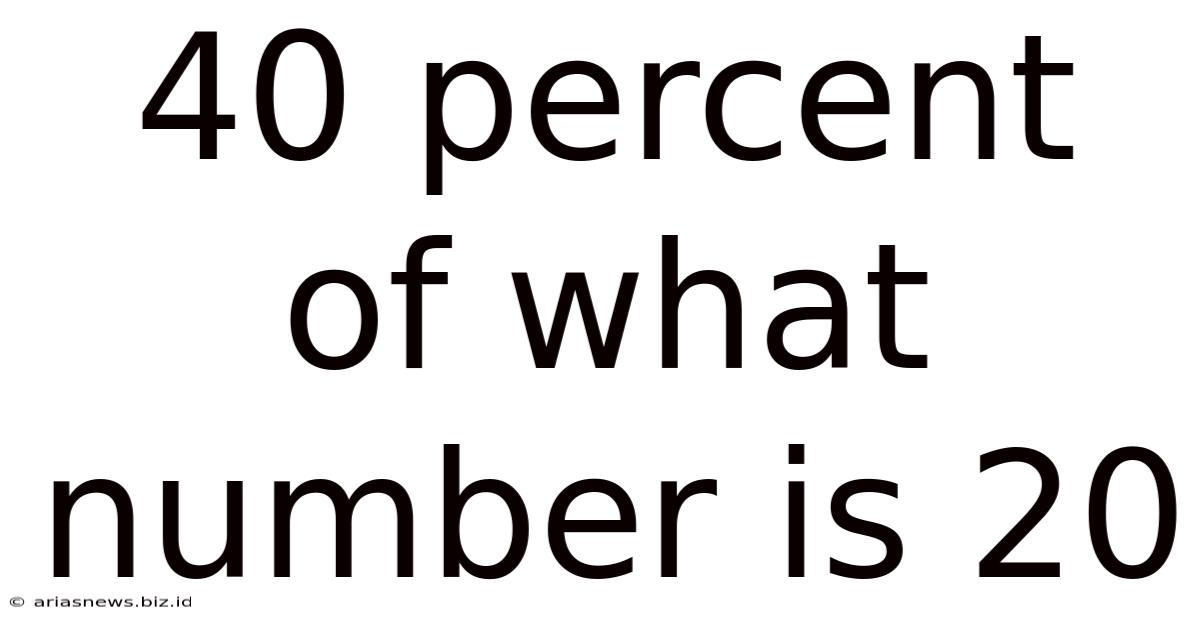
Table of Contents
40 Percent of What Number is 20? Unraveling the Math and its Applications
Finding the answer to "40 percent of what number is 20?" might seem like a simple math problem, but it opens doors to understanding fundamental concepts in percentage calculations, their practical applications in various fields, and even touches on more advanced mathematical concepts. This article will not only provide the solution but delve deeper into the "why" and "how," equipping you with a comprehensive grasp of percentages and their real-world relevance.
Understanding Percentages: The Foundation
Percentages are a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." When we say 40 percent, we're essentially saying 40 out of 100, or 40/100, which simplifies to 2/5. This fractional representation is key to solving percentage problems.
Key Components of Percentage Problems
Every percentage problem has three core components:
- The Percentage: This is the portion of the whole that is being considered (in our case, 40%).
- The Part: This is the numerical value representing the percentage of the whole (in our case, 20).
- The Whole: This is the total amount or the base number we are trying to find (this is what we're solving for).
Solving "40 Percent of What Number is 20?"
We can approach this problem using several methods:
Method 1: Algebraic Approach
Let's represent the unknown whole number as 'x'. We can translate the problem into an algebraic equation:
0.40 * x = 20
To solve for x, we divide both sides of the equation by 0.40:
x = 20 / 0.40
x = 50
Therefore, 40 percent of 50 is 20.
Method 2: Using Proportions
We can set up a proportion to solve this problem:
40/100 = 20/x
Cross-multiplying gives us:
40x = 2000
Dividing both sides by 40:
x = 50
Again, we find that the unknown number is 50.
Method 3: Working with Fractions
As mentioned earlier, 40% is equivalent to 2/5. We can rewrite the problem as:
(2/5) * x = 20
Multiplying both sides by 5/2 (the reciprocal of 2/5):
x = 20 * (5/2)
x = 10 * 5
x = 50
This method reinforces the equivalence between percentages and fractions.
Real-World Applications of Percentage Calculations
The ability to solve percentage problems, like the one we've just tackled, is invaluable across many aspects of life:
1. Finance and Budgeting:
- Calculating discounts: Stores frequently offer discounts expressed as percentages. Understanding how to calculate the actual amount saved is crucial for savvy shopping.
- Determining interest: Interest rates on loans, savings accounts, and investments are expressed as percentages. Knowing how to calculate interest earned or owed is essential for financial planning.
- Analyzing financial statements: Financial reports utilize percentages extensively to represent various ratios and proportions, enabling a clearer understanding of a company's financial health.
- Tax calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
2. Business and Sales:
- Profit margin analysis: Businesses use percentage calculations to determine their profit margins, helping them understand the profitability of their products or services.
- Sales growth calculations: Tracking sales growth as a percentage provides valuable insights into business performance and helps in making informed decisions.
- Market share analysis: Companies use percentages to analyze their market share and understand their position relative to competitors.
- Inventory management: Percentages are utilized to track inventory levels and manage stock effectively.
3. Science and Statistics:
- Data analysis: Percentages are fundamental in representing and interpreting data in various scientific fields, including biology, chemistry, and physics.
- Probability calculations: Probability, often expressed as percentages, is crucial in many scientific and statistical analyses.
- Experimental results: Scientific experiments often involve calculating percentages to represent the success rate or the occurrence of specific events.
4. Everyday Life:
- Tip calculations: Calculating a tip at a restaurant often involves determining a percentage of the total bill.
- Recipe adjustments: Scaling recipes up or down requires understanding how to adjust ingredient quantities based on percentages.
- Understanding surveys and polls: Survey and poll results frequently use percentages to represent the opinions or preferences of a population sample.
Expanding on the Concept: Advanced Applications
The seemingly simple problem of "40 percent of what number is 20?" opens the door to more advanced mathematical concepts:
1. Inverse Percentage Problems:
This problem is a classic example of an inverse percentage problem. Instead of finding a percentage of a number, we find the original number based on a known percentage and its value.
2. Percentage Change:
Understanding percentage change (increase or decrease) builds upon the foundation of basic percentage calculations. This is frequently used to compare values over time or analyze trends.
3. Compound Interest:
Understanding compound interest, where interest is calculated not only on the principal amount but also on accumulated interest, requires a deeper understanding of percentage calculations over time.
4. Exponential Growth and Decay:
Concepts like exponential growth and decay, often seen in fields like finance and biology, rely heavily on percentage calculations to model changes over time.
Conclusion: Mastering Percentages for Success
The solution to "40 percent of what number is 20?" – 50 – might seem straightforward. However, the underlying concepts and their wide-ranging applications extend far beyond this single problem. Mastering percentage calculations equips you with essential skills applicable in numerous professional and personal contexts. From managing finances and interpreting data to making informed decisions in business and everyday life, the ability to confidently work with percentages is a valuable asset. By understanding the different methods of solving percentage problems and appreciating their practical relevance, you can build a stronger foundation for tackling more complex mathematical challenges and confidently navigating the quantitative aspects of the world around you.
Latest Posts
Latest Posts
-
Can A Triangle Have Two Right Angles
May 10, 2025
-
Data In Order From Smallest To Largest Or Vice Versa
May 10, 2025
-
What Is The Greatest Common Factor Of 16 And 24
May 10, 2025
-
How Many Watts Is 120 Vac 60 Hz
May 10, 2025
-
How Long Does V8 Juice Last Unopened
May 10, 2025
Related Post
Thank you for visiting our website which covers about 40 Percent Of What Number Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.