5 Is 25 Percent Of What Number
Arias News
May 08, 2025 · 4 min read
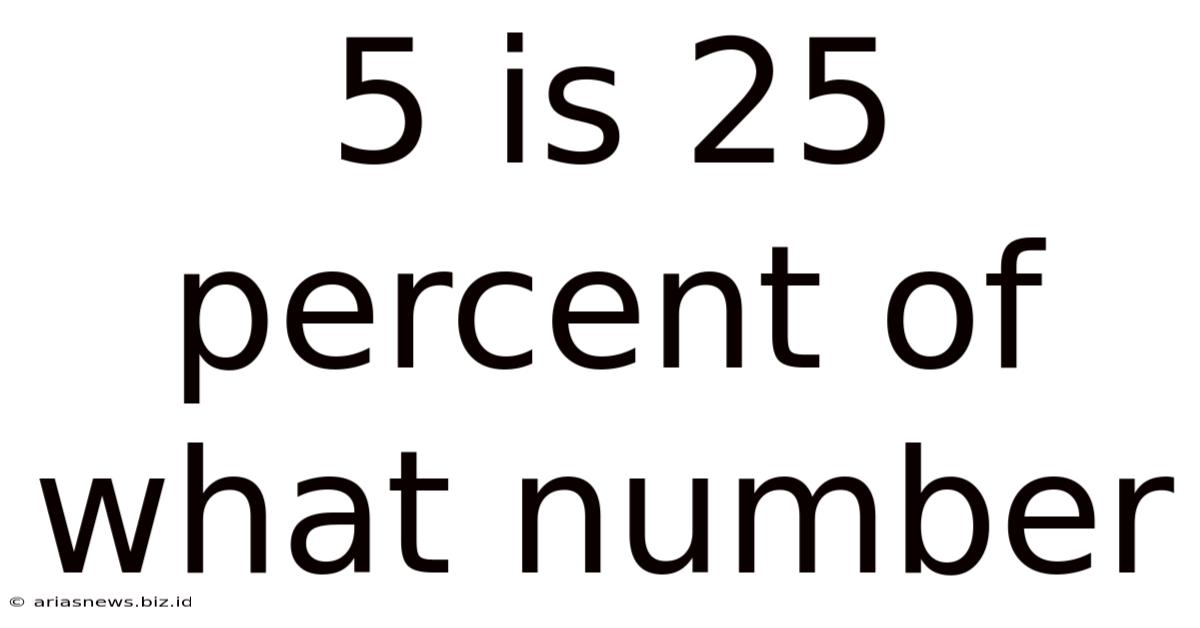
Table of Contents
5 is 25 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Percentages are a fundamental part of mathematics and are used extensively in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. One common type of percentage problem involves finding the whole number when a percentage of it is known. This article will delve into the question, "5 is 25 percent of what number?", providing a step-by-step solution, exploring different methods, and expanding on the broader concept of percentage calculations.
Understanding Percentages
Before we dive into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred." For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Solving "5 is 25 Percent of What Number?"
The core of this problem lies in translating the statement into a mathematical equation. The statement "5 is 25 percent of what number?" can be written as:
5 = 0.25 * x
Where 'x' represents the unknown number we are trying to find.
Method 1: Algebraic Solution
This is the most straightforward method. We solve for 'x' by isolating it on one side of the equation:
-
Divide both sides by 0.25: This will isolate 'x'. 5 / 0.25 = x
-
Calculate the result: 5 divided by 0.25 equals 20.
Therefore, x = 20. 5 is 25 percent of 20.
Method 2: Using Proportions
Proportions offer a visual and intuitive approach to solving percentage problems. We can set up a proportion as follows:
5/x = 25/100
This proportion states that the ratio of 5 to the unknown number (x) is equal to the ratio of 25 to 100 (which represents 25%).
To solve this proportion:
-
Cross-multiply: Multiply 5 by 100 and 25 by x. This gives us: 500 = 25x
-
Solve for x: Divide both sides by 25: 500 / 25 = x
-
Calculate the result: 500 divided by 25 equals 20.
Again, we find that x = 20.
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our problem, we know the part (5) and the percentage (25%). We need to find the whole (x). We can rearrange the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting our values:
Whole = (5 / 25) * 100 = 20
This method confirms our previous findings.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
- Retail Discounts: Calculating discounts offered during sales. For instance, a 20% discount on a $50 item.
- Tax Calculations: Determining sales tax or income tax amounts.
- Financial Analysis: Interpreting financial statements, including profit margins, interest rates, and investment returns.
- Statistics: Understanding statistical data and probabilities often involves percentage calculations.
- Scientific Measurements: Expressing changes or proportions in scientific experiments and data analysis.
- Surveys and Polls: Analyzing survey results and interpreting poll data often uses percentage representation.
- Cooking and Baking: Scaling recipes up or down based on percentage changes.
Expanding on Percentage Concepts
Let's explore some related percentage concepts to build a more comprehensive understanding:
Finding the Percentage Increase or Decrease
This involves calculating the percentage change between two numbers. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
A positive result indicates an increase, while a negative result indicates a decrease.
Calculating Percentage Points
Percentage points represent the arithmetic difference between two percentages. For example, if the interest rate increases from 5% to 8%, it's a 3-percentage-point increase, not a 60% increase.
Compound Interest
Compound interest involves earning interest on both the principal amount and accumulated interest. This results in exponential growth over time. The formula is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Advanced Percentage Problems and Strategies
While the initial problem was relatively straightforward, percentage problems can become more complex. Here are some advanced strategies:
-
Using a calculator: For more complex calculations, a scientific calculator can simplify the process and reduce errors.
-
Breaking down complex problems: Large or multi-step problems can be broken down into smaller, manageable parts.
-
Visual aids: Diagrams, charts, and graphs can be helpful in visualizing and understanding percentage relationships.
-
Practice: The more you practice solving percentage problems, the more comfortable and efficient you'll become.
Conclusion
The ability to solve percentage problems is a valuable skill with broad applications. Understanding the different methods—algebraic solutions, proportions, and the percentage formula—provides flexibility in approaching various problems. Mastering these techniques enables confident navigation of everyday situations involving percentages, from financial transactions to data interpretation. By consistently applying these methods and continuously practicing, you can build a strong foundation in percentage calculations and effectively utilize them in numerous contexts. Remember, the core principle is translating the word problem into a mathematical equation, and then applying the appropriate algebraic or proportional methods to solve for the unknown variable.
Latest Posts
Latest Posts
-
After Katniss Suggested An Alliance Rue Said She Could
May 11, 2025
-
Find The Greatest Common Factor Of 110 40 And 120
May 11, 2025
-
How To Reheat Chicken Parm In Oven
May 11, 2025
-
Cif Number In Central Bank Of India
May 11, 2025
-
How To Say Thank You In Afrikaans
May 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Is 25 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.