5 Is Added To The Cube Of A Number.
Arias News
May 11, 2025 · 5 min read
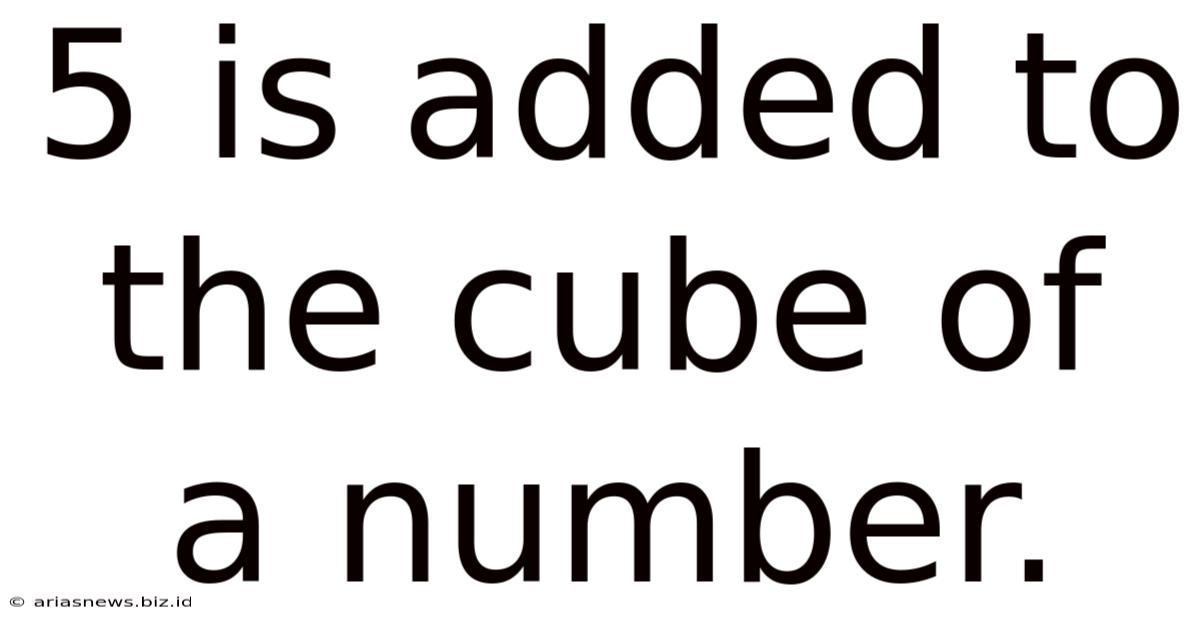
Table of Contents
5 is Added to the Cube of a Number: Exploring Mathematical Concepts and Applications
The seemingly simple phrase "5 is added to the cube of a number" opens the door to a surprisingly rich exploration of mathematical concepts, from basic algebra to more advanced areas like calculus and number theory. This seemingly simple statement forms the basis for numerous problems, equations, and even real-world applications. Let's delve into the intricacies of this mathematical expression, exploring its various interpretations and implications.
Understanding the Core Expression: x³ + 5
At its heart, the phrase "5 is added to the cube of a number" translates directly into the algebraic expression: x³ + 5. Here, 'x' represents the unknown number, 'x³' signifies its cube (the number multiplied by itself three times), and '+ 5' indicates the addition of 5 to the result. This simple expression provides the foundation for a multitude of mathematical investigations.
Exploring Different Values of x
The beauty of this expression lies in its versatility. By substituting different values for 'x', we obtain diverse results, each revealing different aspects of the equation's behavior.
- x = 0: 0³ + 5 = 5. This illustrates the simplest scenario.
- x = 1: 1³ + 5 = 6. A straightforward addition.
- x = 2: 2³ + 5 = 13. The result increases significantly as 'x' grows.
- x = -1: (-1)³ + 5 = 4. The cube of a negative number is negative, but adding 5 leads to a positive result.
- x = -2: (-2)³ + 5 = -3. A negative result is obtained for this negative value of x.
These simple substitutions demonstrate the fundamental relationship between 'x' and the resultant value of the expression. The expression is a cubic function, meaning its graph will have a characteristic S-shape, reflecting the cubic power of x.
Graphical Representation and Analysis
Visualizing the function x³ + 5 through a graph provides a deeper understanding of its behavior. The graph reveals several key characteristics:
- Continuous and Smooth: The function is continuous, meaning there are no breaks or jumps in the graph. It's also smooth, without any sharp corners or cusps. This reflects the smooth nature of the cubic function.
- Increasing Function: As 'x' increases, the value of x³ + 5 also increases. This is a key property of the function.
- One Real Root: The graph intersects the x-axis at only one point. This is the real root of the equation x³ + 5 = 0, which can be found by solving for x: x = ∛(-5) This represents approximately -1.71.
- Symmetry: While not perfectly symmetrical, the graph exhibits a certain symmetry around the inflection point which can be found through calculus. We can observe that negative values of x produce significantly smaller values of the expression than positive values of x.
The graph helps to visualize the behavior of the equation and to understand how changes in 'x' affect the output.
Solving Equations Involving x³ + 5
The expression x³ + 5 can be part of more complex equations. Let's explore some examples and their solution strategies.
Example 1: x³ + 5 = 14
To solve this, we isolate x³:
x³ = 14 - 5 x³ = 9 x = ∛9
This provides the exact solution. Approximating this value provides an approximate solution.
Example 2: x³ + 5 = 0
This is a simpler case leading to:
x³ = -5 x = ∛(-5) ≈ -1.71
This reveals the single real root mentioned previously.
Example 3: More Complex Equations
The expression can be integrated into more intricate equations, often requiring more advanced techniques to solve. For instance:
2(x³ + 5) + 7x = 15
This equation would require expansion, rearrangement, and potentially numerical methods to solve accurately. Such complex equations often don't have easy algebraic solutions and may require numerical methods to approximate the solutions for x.
Applications in Various Fields
While the expression itself might seem abstract, its underlying principles have several applications in diverse fields:
- Physics: Cubic functions frequently model physical phenomena, such as the relationship between force and displacement in certain systems. Adding the constant 5 could represent an offset or initial condition.
- Engineering: Cubic equations are encountered in structural analysis, fluid dynamics, and other engineering problems where the cubic relationship is fundamental to the system being modeled.
- Computer Graphics: Cubic curves and surfaces are commonly used in computer graphics to create smooth, realistic shapes. The addition of a constant like 5 might adjust the position or scaling of the curve or surface.
- Economics: Economic models sometimes use cubic functions to represent factors such as production, cost, and profit.
- Chemistry: The cubic function can sometimes be useful in modeling chemical reaction rates or other processes.
Expanding the Exploration: Calculus and Beyond
A more advanced exploration of x³ + 5 would involve applying calculus. We can derive the function's derivative, which represents the instantaneous rate of change. The first derivative (3x²) shows the rate at which the function is increasing or decreasing. The second derivative (6x) provides information about the concavity of the function (whether it curves upwards or downwards). These insights are valuable in analyzing the function's behavior and identifying points of inflection or extrema.
Conclusion
The seemingly basic mathematical expression "5 is added to the cube of a number" offers a surprisingly rich arena for exploration. From simple algebraic manipulation and graphical representation to the application of calculus and its use in diverse fields, this expression showcases the interconnectedness of mathematical concepts and their relevance in the real world. Its simplicity belies its power, revealing how fundamental mathematical principles form the building blocks of complex systems and applications. Further investigation, involving more complex equations or exploring different functions related to the cube and addition, will continue to uncover deeper mathematical insights. The journey of understanding this expression demonstrates that even seemingly simple ideas can lead to a vast and exciting realm of mathematical discovery.
Latest Posts
Latest Posts
-
2 To The 3 To The 4
May 11, 2025
-
What Do The Four Terrestrial Planets Have In Common
May 11, 2025
-
50 Lb Of Sand In Cubic Feet
May 11, 2025
-
How Many Miles Does A Smart Car Last
May 11, 2025
-
Square Root Of 7 Rational Or Irrational
May 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Is Added To The Cube Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.