5 Less Than 3 Times A Number
Arias News
May 11, 2025 · 5 min read
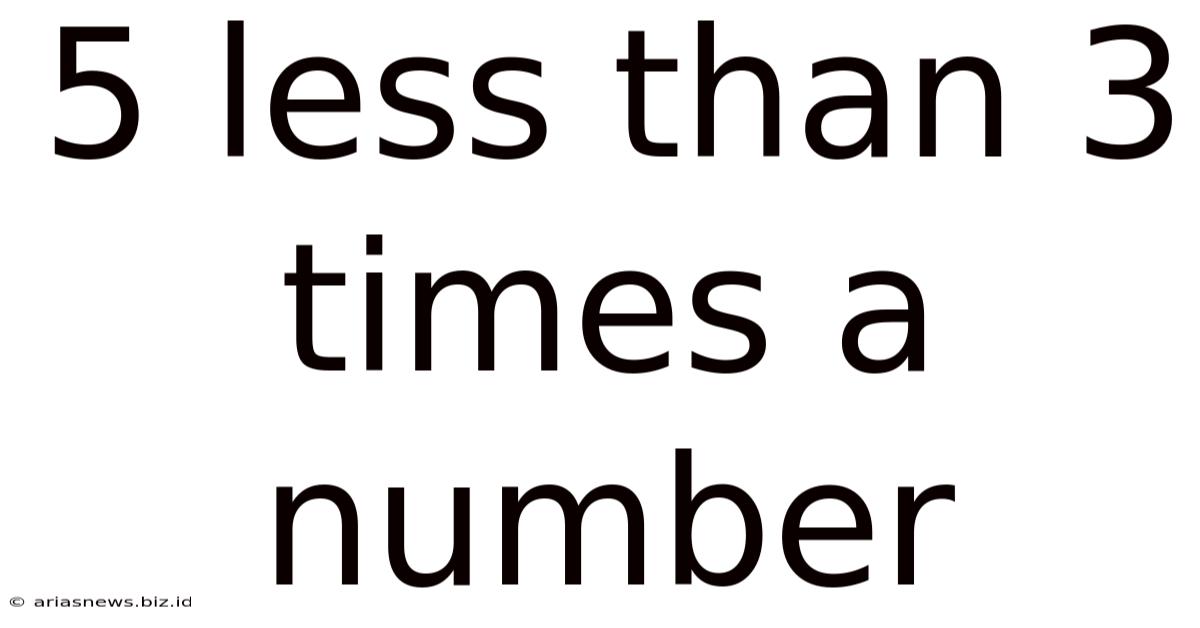
Table of Contents
5 Less Than 3 Times a Number: A Deep Dive into Algebraic Expressions
The seemingly simple phrase, "5 less than 3 times a number," hides a wealth of mathematical concepts and applications. Understanding how to translate this phrase into an algebraic expression is fundamental to algebra and beyond, serving as a building block for more complex equations and problem-solving scenarios. This article will explore this seemingly simple phrase in detail, examining its structure, its applications in various mathematical contexts, and its significance in developing algebraic reasoning.
Understanding the Language of Math
Before diving into the algebraic representation, let's dissect the meaning of the phrase itself. The core components are:
-
"A number": This represents an unknown value, typically denoted by a variable, most commonly 'x'. However, other variables like 'y', 'n', or even more descriptive variables could be used depending on the context of the problem.
-
"3 times a number": This translates directly to multiplication. "3 times a number" becomes 3 * x, or more simply, 3x.
-
"5 less than": This indicates subtraction. However, the order of subtraction is crucial. "5 less than 3x" means we start with 3x and subtract 5 from it. This is not the same as "5 minus 3 times a number," which would be 5 - 3x.
Translating the Phrase into an Algebraic Expression
Combining these elements, the phrase "5 less than 3 times a number" translates to the algebraic expression:
3x - 5
This simple expression encapsulates the entire meaning of the phrase. It's a concise and powerful representation that allows us to perform mathematical operations and solve for the unknown variable, 'x'.
Applications and Problem Solving
This seemingly simple expression has wide-ranging applications in problem-solving across numerous fields. Consider these examples:
Example 1: Finding the Number
Let's say the expression 3x - 5 equals 16. To find the value of 'x', we set up an equation:
3x - 5 = 16
Solving for 'x' involves a series of algebraic manipulations:
- Add 5 to both sides: 3x = 21
- Divide both sides by 3: x = 7
Therefore, the number is 7. We can check our answer by substituting x = 7 back into the original expression: 3(7) - 5 = 16. The equation holds true.
Example 2: Real-World Applications
Imagine a scenario where a fruit vendor sells apples for $3 each. They also have a $5 discount on the total cost if a customer buys a certain number of apples. The total cost (C) can be expressed as:
C = 3x - 5
Where 'x' is the number of apples purchased. This allows the vendor to quickly calculate the cost based on the number of apples sold. For instance, if a customer buys 10 apples, the cost would be:
C = 3(10) - 5 = $25
Example 3: Geometry
The expression could even represent geometrical relationships. For instance, imagine a rectangle where the length is 3 times a certain value and the width is 5 units less than the length. The area (A) of the rectangle could be expressed as:
A = (3x)(3x - 5)
This demonstrates how the expression can be used as a component within a larger mathematical problem.
Expanding the Concept: Variations and Extensions
The core concept of "5 less than 3 times a number" can be expanded and adapted to create more complex expressions. Consider these variations:
-
"10 less than twice a number": This translates to 2x - 10.
-
"7 more than 4 times a number": This translates to 4x + 7. Note the difference in the order of operations compared to the original phrase.
-
"The difference between 3 times a number and 5": This is the same as the original expression: 3x - 5. This highlights the importance of careful attention to wording.
-
Incorporating more variables: Imagine a scenario where the discount varies. The cost expression could become:
C = 3x - d where 'd' represents the variable discount.
This flexibility demonstrates the power of algebraic expressions in modelling real-world situations with varying parameters.
Connecting to Higher-Level Mathematical Concepts
The simple expression 3x - 5 lays the foundation for understanding more advanced mathematical concepts:
-
Functions: The expression can be considered a linear function, where the output (y) is determined by the input (x): y = 3x - 5. This forms the basis for graphing linear equations and understanding function notation.
-
Equations and Inequalities: The expression can be used to form equations (e.g., 3x - 5 = 10) or inequalities (e.g., 3x - 5 > 0). Solving these equations and inequalities requires the application of fundamental algebraic techniques.
-
Calculus: While seemingly unrelated, the concept of derivatives and integrals in calculus builds upon a solid understanding of algebraic expressions like this.
Developing Algebraic Reasoning
Mastering the translation of phrases like "5 less than 3 times a number" is critical for developing strong algebraic reasoning skills. This involves:
-
Careful Reading and Comprehension: Understanding the nuances of language is essential to accurately translate word problems into mathematical expressions.
-
Identifying Key Words: Words like "times," "less than," "more than," "plus," and "minus" are key indicators of mathematical operations.
-
Order of Operations (PEMDAS/BODMAS): Understanding the order of operations ensures calculations are performed correctly.
-
Practice: Consistent practice with various word problems strengthens the ability to translate words into algebraic symbols and solve equations.
Conclusion: The Power of Simplicity
The phrase "5 less than 3 times a number" might seem simplistic at first glance. However, it serves as a powerful entry point to the world of algebra. Understanding its structure, applications, and extensions illuminates the fundamental principles of algebraic reasoning and problem-solving. By mastering the translation of this phrase and similar expressions, students develop a strong foundation for tackling more complex mathematical challenges across various academic disciplines and real-world situations. The seemingly simple algebraic expression 3x - 5 is a cornerstone in the journey of mathematical understanding, showcasing the power and elegance of mathematical language. It underscores the importance of translating everyday language into precise mathematical representations, a key skill for anyone seeking to master mathematical concepts. Through diligent practice and a thorough understanding of the underlying principles, this seemingly simple expression opens doors to a wealth of mathematical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5 Less Than 3 Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.