5 Less Than The Square Of A Number.
Arias News
May 11, 2025 · 5 min read
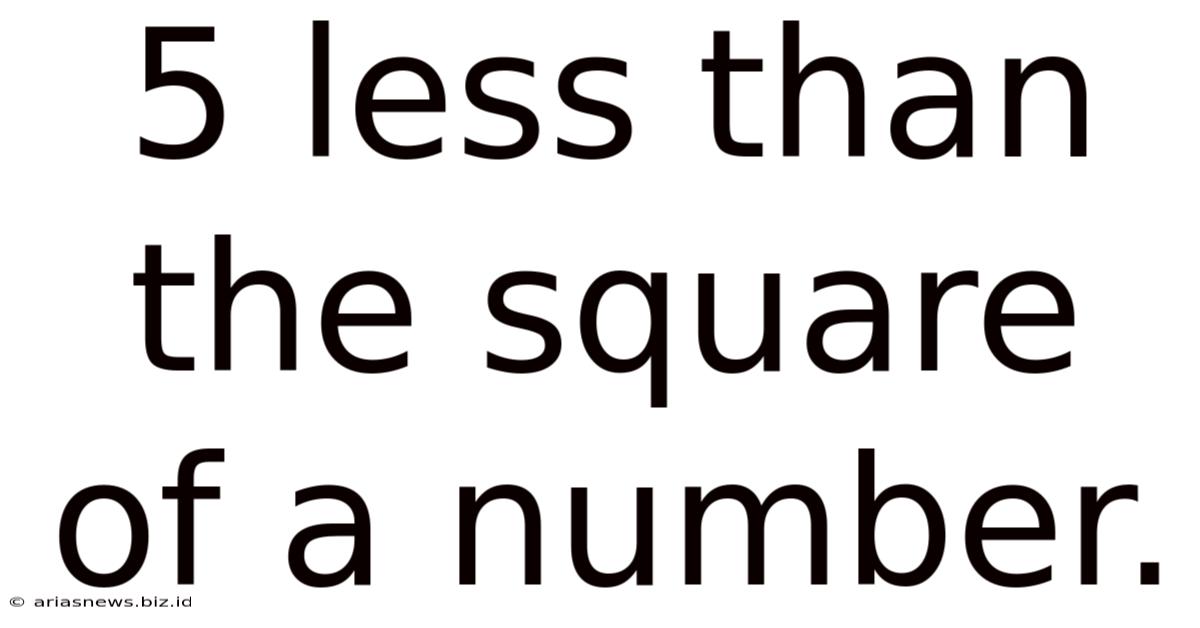
Table of Contents
5 Less Than the Square of a Number: Exploring Quadratic Equations and Their Applications
The seemingly simple phrase "5 less than the square of a number" hides a wealth of mathematical richness. This expression, easily translated into the algebraic equation x² - 5, opens doors to exploring quadratic equations, their solutions, and their surprising applications in various fields. This article will delve deep into this seemingly simple concept, unraveling its complexities and showcasing its significance in mathematics and beyond.
Understanding the Quadratic Equation: x² - 5 = 0
The core of our exploration lies in the quadratic equation derived from the phrase: x² - 5 = 0. This is a fundamental quadratic equation in its simplest form. Understanding its structure is key to unlocking its potential.
Defining Key Terms
-
Quadratic Equation: An equation of the form ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our equation, x² - 5 = 0, fits this form with a = 1, b = 0, and c = -5.
-
Variable (x): The unknown quantity we aim to solve for. In this context, 'x' represents the number we're seeking.
-
Constants (a, b, c): The fixed numerical values in the equation.
-
Roots or Solutions: The values of x that satisfy the equation (make the equation true). Finding these roots is the primary goal when solving a quadratic equation.
Methods for Solving x² - 5 = 0
Several methods exist for solving quadratic equations. Let's explore the most common approaches applied to our specific equation, x² - 5 = 0.
1. Square Root Method
This is the simplest method for solving our equation because it lacks a linear term (bx). We can directly manipulate the equation:
x² = 5
Taking the square root of both sides:
x = ±√5
This gives us two solutions: x = √5 and x = -√5. These are irrational numbers, meaning they cannot be expressed as a simple fraction. Their approximate decimal values are x ≈ 2.236 and x ≈ -2.236.
2. Quadratic Formula
The quadratic formula is a more general method applicable to all quadratic equations, regardless of the presence of a linear term. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our equation (a = 1, b = 0, c = -5), the formula simplifies to:
x = [0 ± √(0² - 4 * 1 * -5)] / (2 * 1)
x = ±√20 / 2
x = ±2√5 / 2
x = ±√5
This yields the same solutions as the square root method: x = √5 and x = -√5.
3. Factoring (Not Directly Applicable)
Factoring involves expressing the quadratic equation as a product of two linear expressions. While effective for many quadratic equations, our equation, x² - 5 = 0, doesn't factor neatly using integers or rational numbers. Therefore, this method isn't the most efficient approach in this case.
Graphical Representation and Interpretation
Visualizing the equation x² - 5 = 0 graphically provides valuable insights. The equation represents a parabola, a U-shaped curve. The solutions (roots) are the x-intercepts—the points where the parabola intersects the x-axis.
Parabola Characteristics
-
Vertex: The lowest point of the parabola (in this case, (0, -5)).
-
Axis of Symmetry: A vertical line passing through the vertex (x = 0).
-
X-intercepts: The points where the parabola crosses the x-axis (√5 and -√5). These are the solutions to the equation.
-
Y-intercept: The point where the parabola crosses the y-axis (0, -5).
Applications of Quadratic Equations
The seemingly abstract concept of "5 less than the square of a number" and its corresponding quadratic equation find practical applications in diverse fields:
1. Physics: Projectile Motion
Quadratic equations are essential in describing the trajectory of projectiles under the influence of gravity. The height of a projectile at any given time can often be modeled by a quadratic equation.
2. Engineering: Bridge Design
The parabolic shape of many bridges is described by quadratic equations. Engineers use these equations to calculate the strength and stability of bridge structures.
3. Economics: Optimization Problems
Quadratic equations can model cost functions or revenue functions in business scenarios. Finding the minimum cost or maximum revenue often involves solving a quadratic equation.
4. Computer Graphics: Curve Modeling
Quadratic curves are used extensively in computer graphics to create smooth, curved shapes and animations.
5. Area and Volume Calculations
Problems involving the calculation of areas of shapes (like rectangles with specific area-to-side ratios) and volumes often result in quadratic equations.
Exploring Variations and Extensions
Let's expand our understanding by considering variations of the original expression:
1. "5 More Than the Square of a Number"
This translates to the equation x² + 5 = 0. This equation has no real solutions, as the square of any real number is always non-negative. The solutions are complex numbers: x = ±i√5, where 'i' is the imaginary unit (√-1).
2. "The Square of a Number, Minus 5, Equals 10"
This leads to the equation x² - 5 = 10, or x² = 15. The solutions are x = ±√15.
Conclusion: The Significance of a Simple Expression
The seemingly simple expression, "5 less than the square of a number," opens up a vast landscape of mathematical concepts and real-world applications. From understanding the fundamentals of quadratic equations to applying them in diverse fields like physics, engineering, and economics, the exploration of this expression highlights the power and relevance of mathematics in our world. The ability to translate a simple phrase into a mathematical equation and then solve that equation demonstrates the analytical and problem-solving skills crucial in various disciplines. Furthermore, the visual representation of the equation through its parabola provides a powerful tool for intuitive understanding and interpretation of the results. By mastering the concepts outlined here, one gains a valuable foundation for tackling more complex mathematical challenges and appreciating the beauty and utility of mathematics in its various forms.
Latest Posts
Latest Posts
-
Can Bearded Dragons Eat Brussel Sprout Leaves
May 12, 2025
-
How Many Right Angles Does Trapezoid Have
May 12, 2025
-
Kohler 52 50 02 S Cross Reference
May 12, 2025
-
How Much Is 1 Acre Of Land In Mexico
May 12, 2025
-
Does 7 11 Give Out Free Slurpees Today
May 12, 2025
Related Post
Thank you for visiting our website which covers about 5 Less Than The Square Of A Number. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.