5 Percent As A Fraction In Simplest Form
Arias News
May 11, 2025 · 5 min read
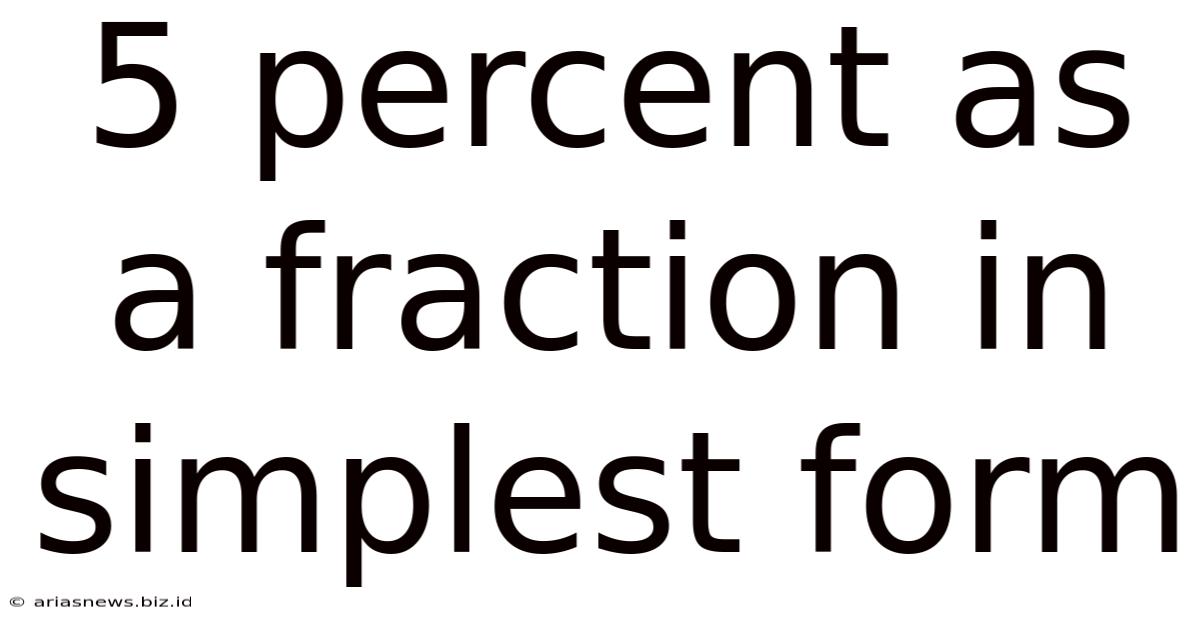
Table of Contents
5 Percent as a Fraction in Simplest Form: A Comprehensive Guide
Understanding percentages, fractions, and decimals is fundamental to various aspects of life, from calculating discounts to comprehending financial reports. This comprehensive guide delves into the conversion of 5 percent to its simplest fraction form, exploring the underlying principles and offering practical examples. We'll also examine the broader context of percentage-to-fraction conversions and their applications in real-world scenarios.
Understanding Percentages and Fractions
Before we tackle the conversion of 5 percent to a fraction, let's briefly review the definitions of percentages and fractions.
Percentage: A percentage represents a fraction of 100. The word "percent" literally means "per hundred." So, 5% means 5 out of 100.
Fraction: A fraction represents a part of a whole. It is expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction ½, 1 is the numerator and 2 is the denominator.
Converting 5 Percent to a Fraction
The conversion of a percentage to a fraction involves two simple steps:
Step 1: Write the percentage as a fraction with a denominator of 100.
5% can be written as the fraction 5/100. This directly reflects the definition of percentage – 5 parts out of 100.
Step 2: Simplify the fraction to its lowest terms.
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In the case of 5/100, the GCD of 5 and 100 is 5. Dividing both the numerator and the denominator by 5, we get:
5 ÷ 5 = 1 100 ÷ 5 = 20
Therefore, 5% as a fraction in its simplest form is 1/20.
Practical Applications of Percentage-to-Fraction Conversions
The ability to convert percentages to fractions is invaluable in numerous situations, both in everyday life and professional contexts. Here are a few examples:
1. Calculating Discounts: Imagine a store offering a 5% discount on an item. Understanding that 5% is equivalent to 1/20 allows for quick mental calculation of the discount. If the item costs $100, the discount is (1/20) * $100 = $5.
2. Understanding Financial Statements: Financial reports often use percentages to represent various ratios and proportions. Converting these percentages to fractions can provide a clearer understanding of the underlying relationships. For example, a company's profit margin of 5% can be interpreted as earning $1 for every $20 in revenue.
3. Baking and Cooking: Recipes often use percentages to indicate the proportion of ingredients. Converting these percentages to fractions can lead to more precise measurements and better results.
4. Probability and Statistics: Probability is often expressed as a percentage. Converting this percentage to a fraction simplifies the calculation of probabilities in various scenarios. For instance, a 5% chance of an event occurring can be represented as a 1/20 probability.
5. Geometry and Mensuration: In certain geometrical calculations, understanding percentages as fractions can help in simplifying complex problems and improve understanding.
Beyond 5 Percent: Generalizing the Conversion Process
The method used to convert 5 percent to a fraction can be applied to any percentage. The steps remain the same:
- Write the percentage as a fraction with a denominator of 100.
- Simplify the fraction to its lowest terms by finding the GCD of the numerator and the denominator and dividing both by it.
Let's look at a few more examples:
- 10%: 10/100 simplifies to 1/10
- 25%: 25/100 simplifies to 1/4
- 75%: 75/100 simplifies to 3/4
- 30%: 30/100 simplifies to 3/10
- 60%: 60/100 simplifies to 3/5
Dealing with Percentages Greater Than 100%
Percentages can also be greater than 100%, representing quantities exceeding the original whole. The conversion process remains the same. For example:
- 150%: 150/100 simplifies to 3/2 or 1 ½
Converting Fractions Back to Percentages
Conversely, it's equally important to know how to convert a fraction back to a percentage. To do this, we simply divide the numerator by the denominator and multiply the result by 100.
For example, to convert 1/20 back to a percentage:
1 ÷ 20 = 0.05 0.05 * 100 = 5%
Advanced Concepts and Applications
The conversion between percentages and fractions lays the groundwork for understanding more advanced mathematical concepts, including:
- Ratio and Proportion: Percentages and fractions are intrinsically linked to ratio and proportion, crucial for problem-solving in various fields.
- Algebra: Understanding fractions and percentages is essential for solving algebraic equations involving ratios and proportions.
- Calculus: The concepts are fundamental for understanding derivatives and integrals, particularly when dealing with rates of change.
Conclusion: Mastering Percentage-to-Fraction Conversions
Mastering the conversion of percentages to fractions, exemplified by the simple yet crucial conversion of 5% to 1/20, is a cornerstone of mathematical literacy. This ability transcends simple calculations and opens doors to a deeper understanding of numerous mathematical concepts and their applications in diverse real-world scenarios. Whether you're dealing with discounts, financial statements, or more complex mathematical problems, the skill of converting percentages to their simplest fraction form proves invaluable. By understanding the underlying principles and practicing the conversion process, you equip yourself with a powerful tool for numerical comprehension and problem-solving. Remember to always simplify your fractions to their lowest terms for the most efficient representation.
Latest Posts
Latest Posts
-
A Metronome Marking Of 200 Would Most Likely Be Labeled
May 12, 2025
-
150 Square Meters Is How Many Square Feet
May 12, 2025
-
What Percent Of The Figure Is Shaded
May 12, 2025
-
21 Out Of 29 As A Percentage
May 12, 2025
-
Why Nh3 Is More Polar Than Nf3
May 12, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.