5 Times The Square Root Of 3
Arias News
Mar 30, 2025 · 5 min read
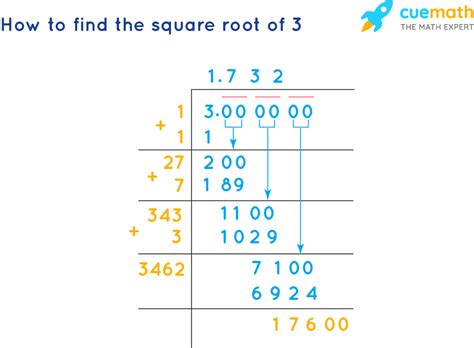
Table of Contents
5 Times the Square Root of 3: Unveiling the Mysteries of 5√3
The seemingly simple expression "5 times the square root of 3" (5√3) holds a surprising depth, connecting seemingly disparate fields of mathematics, geometry, and even physics. This exploration delves into the various facets of this mathematical constant, examining its properties, applications, and significance. We'll move beyond a simple numerical value to understand its role within a broader mathematical landscape.
Understanding the Basics: What is 5√3?
Before diving into complex applications, let's establish a clear understanding of what 5√3 represents. It's a product of two numbers: 5, a whole number, and √3, an irrational number. The square root of 3 (√3) is approximately 1.732. Therefore, 5√3 is approximately 5 * 1.732 = 8.660. This is an irrational number, meaning it cannot be expressed as a simple fraction of two integers. Its decimal representation continues infinitely without repeating.
Key takeaway: 5√3 is an irrational number, approximately equal to 8.660.
Geometric Interpretations: Visualizing 5√3
The beauty of mathematics lies in its ability to connect abstract concepts to the tangible world. 5√3 finds elegant representation in geometry. Consider an equilateral triangle. Its height is related to its side length by the factor of √3/2. If we have an equilateral triangle with a side length of 10 units, its height will be 5√3 units. This provides a practical, visual understanding of this number.
Applications in Geometry:
- Equilateral Triangles: As demonstrated above, calculating the height of an equilateral triangle.
- Hexagons: The height of an equilateral triangle forms the apothem of a regular hexagon. Therefore, understanding 5√3 is crucial for calculating areas and other properties of hexagons.
- Trigonometry: The number appears frequently in trigonometric calculations involving angles of 30, 60, and 120 degrees, due to the relationship between these angles and equilateral triangles.
Algebraic Explorations: Manipulating 5√3
5√3 isn't just a number; it's a mathematical object that can be manipulated algebraically. We can perform various operations with it, including addition, subtraction, multiplication, and division. However, it's crucial to remember that it's an irrational number, which often leads to irrational results even when combined with rational numbers.
Operations with 5√3:
- Addition/Subtraction: Adding or subtracting 5√3 to/from other numbers (rational or irrational) typically results in an irrational number. For example, 5√3 + 2 remains irrational.
- Multiplication: Multiplying 5√3 by another number scales its magnitude. For example, 2 * 5√3 = 10√3.
- Division: Dividing 5√3 by another number reduces its magnitude. For example, 5√3 / 5 = √3.
- Squaring: Squaring 5√3 yields (5√3)² = 25 * 3 = 75. This demonstrates a simplification that occurs when squaring such expressions, transforming an irrational number into a rational one.
Important note: When working with 5√3 in algebraic equations, it's generally best to leave it in its surd form (5√3) unless a decimal approximation is specifically required.
Advanced Applications: Beyond the Basics
The applications of 5√3 extend beyond simple geometric calculations. Its appearance in more complex mathematical contexts highlights its significance.
Trigonometry and Complex Numbers:
5√3 plays a role in solving trigonometric equations and working with complex numbers. Complex numbers, which involve the imaginary unit 'i' (√-1), often include terms involving square roots, including √3. These relationships are particularly apparent in the study of phasors and alternating current (AC) circuits in electrical engineering.
Calculus and Infinite Series:
While not as directly apparent, 5√3 might appear in the results of certain calculus problems or as a term within infinite series. Its presence underscores the interconnectedness of mathematical concepts. The irrational nature of the number doesn't prevent it from participating in complex mathematical processes.
Real-World Applications: Seeing 5√3 in Action
While 5√3 might seem like an abstract concept, it has tangible applications in various fields:
Physics and Engineering:
- Vector Calculations: In physics and engineering, vectors are used to represent quantities with both magnitude and direction. The components of a vector often involve irrational numbers like 5√3, particularly when dealing with angles other than multiples of 90 degrees.
- AC Circuit Analysis: As mentioned before, 5√3 appears in calculations related to AC circuits, reflecting the phase relationships between voltage and current.
- Structural Engineering: Calculations involving stresses, strains, and stability in structures often lead to expressions containing √3, including multiples like 5√3. These calculations ensure the safety and stability of buildings and other structures.
Architecture and Design:
- Hexagonal Structures: The use of hexagonal shapes in architecture and design requires an understanding of the geometrical properties mentioned earlier, where 5√3 plays a key role in dimensions and calculations.
- Tessellations: Creating regular patterns and tessellations (tilings) frequently employs equilateral triangles and hexagons, which intrinsically involve 5√3 in determining dimensions and proportions.
Numerical Approximations and Computational Considerations
In practical applications, an accurate approximation of 5√3 is often sufficient. Using a calculator, we obtain approximately 8.660254. The level of precision needed will depend on the context. In many cases, rounding to a few decimal places is adequate. However, for high-precision engineering or scientific computations, using the full precision available on a computer or calculator is recommended.
Conclusion: The Richness of 5√3
This exploration reveals that the seemingly simple expression "5 times the square root of 3" holds considerable depth and significance. From its geometric representations in equilateral triangles and hexagons to its applications in advanced fields like physics and engineering, 5√3 showcases the interconnectedness of mathematical concepts and their practical relevance in the real world. Understanding its properties and applications enhances mathematical comprehension and provides a foundation for further exploration into the fascinating world of irrational numbers and their profound implications. Further investigation into the broader contexts where this number appears will undoubtedly reveal even more of its richness and mathematical beauty. The seemingly simple number, 5√3, serves as a potent reminder of the elegance and utility of mathematics in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
How Many Times Does 5 Go Into 100
Apr 01, 2025
-
Is 11 16 Bigger Than 3 4
Apr 01, 2025
-
How Many Feet Is 1 3 Acre
Apr 01, 2025
-
What Is 10 Percent Of 400 000
Apr 01, 2025
-
How Many Verses In The Book Of Revelation
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about 5 Times The Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
