56 Out Of 100 As A Percentage
Arias News
May 11, 2025 · 5 min read
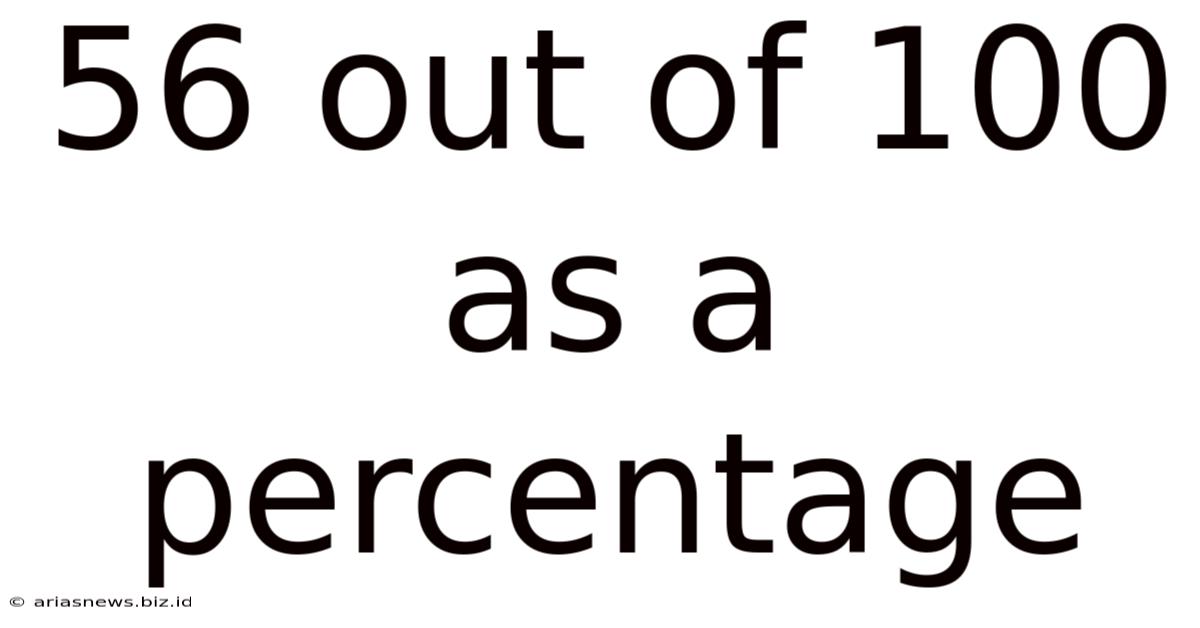
Table of Contents
56 out of 100 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with broad applications in various fields. Understanding how to do this accurately is crucial for tasks ranging from calculating grades and discounts to analyzing data and interpreting statistical information. This comprehensive guide will delve into how to calculate 56 out of 100 as a percentage, explain the underlying principles, and offer practical examples to solidify your understanding.
Understanding Percentages
A percentage is simply a fraction or ratio expressed as a portion of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100. For instance, 50% is equivalent to 50/100, which simplifies to 1/2.
Calculating 56 out of 100 as a Percentage
The calculation of 56 out of 100 as a percentage is straightforward. Since percentages are based on a denominator of 100, this specific problem provides a direct conversion.
Method 1: Direct Conversion
Since we already have the fraction 56/100, converting it to a percentage is simply a matter of adding the percent symbol. Therefore, 56 out of 100 is 56%.
Method 2: Using the Formula
The general formula for calculating a percentage is:
(Part / Whole) x 100%
In this case:
- Part: 56
- Whole: 100
Substituting these values into the formula:
(56 / 100) x 100% = 56%
This method confirms our initial calculation.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is essential in a wide array of real-world situations. Here are some practical examples:
1. Academic Performance
Imagine a student scored 56 out of 100 on a test. Understanding that this equates to 56% allows for easy assessment of their performance relative to the total possible marks. This percentage can then be compared to other scores or grading scales.
2. Discounts and Sales
Retailers often advertise discounts as percentages. If a store offers a 56% discount on an item, calculating the final price involves subtracting 56% of the original price from the original price. This requires converting the percentage back into a decimal (0.56) for the calculation.
3. Financial Analysis
In finance, percentages are used extensively. Calculating interest rates, returns on investments, and analyzing financial statements all rely heavily on understanding percentage calculations. For example, a 56% increase in profit over the previous year is a significant indicator of business success.
4. Data Analysis and Statistics
Percentages are crucial for interpreting data and drawing conclusions. For instance, a survey showing that 56% of respondents prefer a particular product provides valuable insights into consumer preferences. This allows companies to tailor their marketing strategies and product development based on the data.
5. Everyday Calculations
Percentage calculations aren't limited to complex financial models or academic settings. They are used frequently in daily life:
- Calculating tips: Determining the appropriate tip amount at a restaurant often involves calculating a percentage of the total bill.
- Estimating proportions: Determining the percentage of a container filled with a liquid or the percentage of a task completed are common estimations using this method.
- Understanding tax rates: Understanding the tax rate (e.g., sales tax) and calculating the final price of an item after tax requires percentage calculations.
Beyond 56 out of 100: Calculating Other Percentages
While the 56 out of 100 example is straightforward, understanding the broader principles allows for calculating percentages from any fraction. Let's look at how to handle other scenarios:
Calculating Percentages from Fractions with Different Denominators
If the denominator is not 100, you must first convert the fraction into an equivalent fraction with a denominator of 100 or use the formula:
(Part / Whole) x 100%
For example, to find the percentage representation of 14 out of 25:
(14 / 25) x 100% = 56%
This demonstrates that the percentage calculation isn't limited to fractions with a denominator of 100.
Calculating the Part When the Percentage and Whole are Known
Sometimes, you know the percentage and the whole but need to find the part. For example, what is 56% of 200?
(56/100) x 200 = 112
Calculating the Whole When the Percentage and Part are Known
In other scenarios, the percentage and the part are known, and the whole needs to be determined. For example, if 56% of a number is 140, what is the number?
Let 'x' represent the whole. The equation becomes:
(56/100) * x = 140
Solving for x:
x = (140 * 100) / 56 = 250
Advanced Percentage Applications
Beyond the basic calculations, percentages are used in more advanced mathematical and statistical concepts:
- Compound interest: Calculating the future value of an investment considering interest earned on both principal and accumulated interest involves compounding percentages.
- Statistical analysis: Percentages are used to represent proportions, frequencies, and probabilities in various statistical analyses.
- Financial modeling: Complex financial models used to predict future outcomes or evaluate investment opportunities rely on intricate percentage-based calculations.
Conclusion
Understanding how to calculate 56 out of 100 as a percentage, and more broadly, how to calculate percentages in general, is a foundational skill with significant real-world applications. Mastering this skill empowers you to tackle a variety of problems across various disciplines, from everyday budgeting to sophisticated financial analysis. Remember the simple formula, (Part / Whole) x 100%, and you'll be well-equipped to handle any percentage calculation. Practicing these calculations regularly will enhance your proficiency and build your confidence in tackling more complex percentage-related challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about 56 Out Of 100 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.