7 Is 25 Percent Of What In Math
Arias News
May 12, 2025 · 5 min read
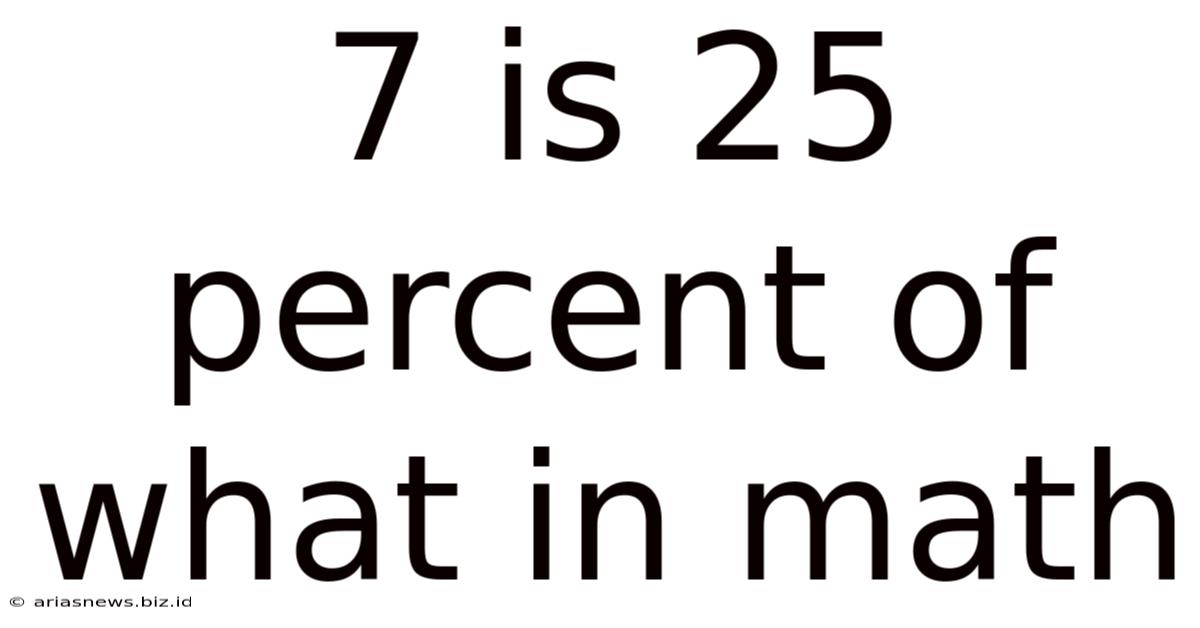
Table of Contents
7 is 25 Percent of What? A Comprehensive Guide to Percentage Calculations
Many everyday situations require understanding percentages. Whether you're calculating discounts, figuring out tips, or tackling more complex mathematical problems, mastering percentage calculations is crucial. This comprehensive guide will walk you through how to solve the problem "7 is 25 percent of what?" and will equip you with the skills to tackle similar percentage problems with confidence. We’ll explore various methods, from simple algebraic solutions to practical real-world applications.
Understanding Percentages: The Fundamentals
Before diving into the problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Understanding this fundamental concept is key to solving percentage problems effectively. Many people struggle with percentages because they don't grasp this basic relationship between percentages, fractions, and decimals. Remember, they are all interchangeable representations of the same value.
Method 1: Using Algebra to Solve "7 is 25% of What?"
The most straightforward method to solve "7 is 25% of what?" involves setting up an algebraic equation. Let's represent the unknown number as 'x'. We can then translate the problem into an equation:
7 = 0.25 * x
This equation states that 7 is equal to 25% (or 0.25) of an unknown number 'x'. To solve for 'x', we simply need to isolate it:
x = 7 / 0.25
Performing the division:
x = 28
Therefore, 7 is 25% of 28.
Method 2: Using Proportions to Solve Percentage Problems
Another effective method for solving percentage problems is using proportions. A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve "7 is 25% of what?" as follows:
7/x = 25/100
This proportion states that the ratio of 7 to the unknown number (x) is equal to the ratio of 25 to 100 (which is equivalent to 25%). To solve for x, we can cross-multiply:
7 * 100 = 25 * x
700 = 25x
x = 700 / 25
x = 28
Again, we arrive at the solution: 7 is 25% of 28. The proportion method offers a visual way to understand the relationship between the known and unknown values.
Method 3: Using the Percentage Formula
A more generalized approach involves using the standard percentage formula:
Percentage = (Part / Whole) * 100
In our problem, we know the percentage (25%) and the part (7). We need to find the whole (x). Rearranging the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting our known values:
Whole = (7 / 25) * 100
Whole = 0.28 * 100
Whole = 28
This confirms once more that 7 is 25% of 28. This formula is highly versatile and can be adapted to solve for any of the three variables (percentage, part, or whole) given the other two.
Real-World Applications: Putting Percentage Calculations to Use
Understanding how to solve percentage problems like "7 is 25% of what?" has numerous practical applications in everyday life:
1. Calculating Discounts:
Imagine a store offers a 25% discount on an item originally priced at $x. If the discount amount is $7, you can use the same method to find the original price ($x):
7 = 0.25 * x x = 28
Therefore, the original price of the item was $28.
2. Determining Sales Tax:
Suppose you pay $7 in sales tax on a purchase, and the tax rate is 25%. You can calculate the original purchase price using the same principles:
7 = 0.25 * x x = 28
The original price before tax was $28.
3. Calculating Tips:
If you leave a 25% tip of $7 at a restaurant, you can determine the pre-tip cost of your meal using the same technique.
4. Analyzing Financial Statements:
Percentage calculations are fundamental in analyzing financial reports. For example, you might calculate the percentage of revenue from a specific product line or the percentage change in profits year over year.
5. Scientific and Engineering Applications:
Percentages play a critical role in many scientific and engineering fields. For instance, calculating the percentage error in experimental measurements or determining the percentage composition of a mixture.
Beyond the Basics: Tackling More Complex Percentage Problems
While "7 is 25% of what?" provides a good foundation, many percentage problems are more intricate. These often involve multiple steps or require working with more than one percentage. Here are some examples of more complex percentage problems:
- Finding the percentage increase or decrease: This involves calculating the percentage change between two values.
- Calculating compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest.
- Solving problems involving multiple percentages: For example, calculating the final price after multiple discounts or tax rates.
Solving these complex problems typically requires a deeper understanding of algebraic manipulations and the application of appropriate formulas. Mastering the fundamental approach shown in this article will provide a strong base for tackling these more challenging situations.
Mastering Percentages: Tips for Success
- Practice Regularly: The key to mastering percentages is consistent practice. Work through various problems, starting with simple ones and gradually increasing the complexity.
- Visualize the Problem: Draw diagrams or use other visual aids to help you understand the relationship between the different parts of the problem.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Use a Calculator: For more complex problems, using a calculator can save time and reduce the risk of errors.
- Seek Help When Needed: Don't hesitate to ask for help if you get stuck. There are many resources available, such as online tutorials, textbooks, and tutors.
By understanding the fundamental principles of percentage calculations and practicing regularly, you can confidently tackle various percentage problems in both mathematical and real-world contexts. The ability to perform these calculations effectively is a valuable skill applicable across numerous fields and essential for navigating everyday financial and analytical tasks. The seemingly simple problem of "7 is 25 percent of what?" serves as a stepping stone towards mastering a critical skill applicable throughout life.
Latest Posts
Related Post
Thank you for visiting our website which covers about 7 Is 25 Percent Of What In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.