7 Out Of 18 As A Percentage
Arias News
May 11, 2025 · 5 min read
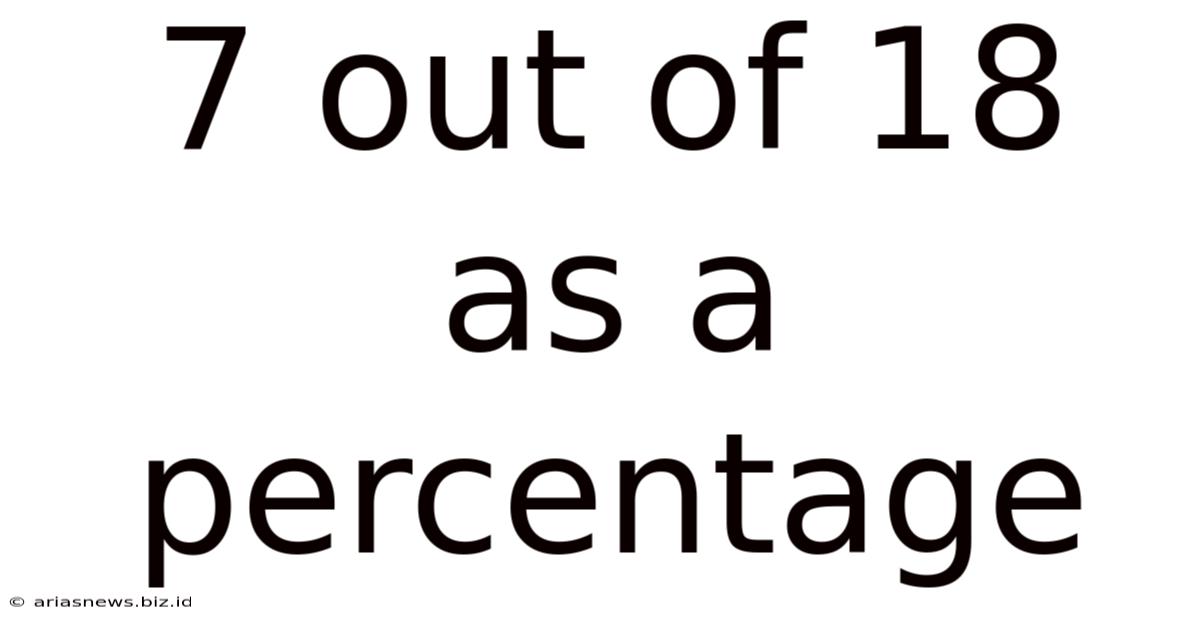
Table of Contents
7 out of 18 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific research. Understanding how to convert fractions into percentages is crucial for accurate data interpretation and informed decision-making. This article delves into the specific calculation of "7 out of 18 as a percentage," providing a step-by-step guide, exploring related concepts, and offering practical applications.
Understanding Percentages
A percentage represents a proportion or fraction of a whole, expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For instance, 50% represents 50 out of 100, or half. This concept is widely used to represent proportions, changes, and rates in diverse contexts.
Calculating 7 out of 18 as a Percentage
To determine the percentage that 7 represents out of 18, we employ a straightforward three-step process:
Step 1: Form a Fraction
First, express the given information as a fraction: 7/18. This fraction signifies 7 parts out of a total of 18 parts.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (7) by the denominator (18):
7 ÷ 18 ≈ 0.3889
Note: We've rounded the decimal to four decimal places for accuracy. The level of rounding will depend on the required precision of your application. For most purposes, rounding to two or three decimal places is sufficient.
Step 3: Convert the Decimal to a Percentage
Finally, multiply the decimal by 100 to express it as a percentage:
0.3889 × 100 = 38.89%
Therefore, 7 out of 18 is approximately 38.89%.
Practical Applications: Where This Calculation Is Used
The calculation of percentages finds widespread applications across numerous fields:
1. Business and Finance
- Profit margins: Businesses utilize percentages to calculate profit margins—the difference between revenue and costs, expressed as a percentage of revenue.
- Sales growth: Tracking sales growth year-over-year or comparing sales performance across different periods often involves percentage calculations.
- Investment returns: Investors utilize percentages to assess the return on their investments, comparing the profit earned against the initial investment.
- Interest rates: Interest rates on loans and savings accounts are typically expressed as percentages.
- Discount calculations: Retailers often advertise discounts as percentages, requiring consumers to calculate the discounted price.
2. Education and Academics
- Grade calculations: Students' final grades are often determined by calculating the percentage of correct answers on exams and assignments.
- Statistical analysis: Percentages are fundamental in analyzing survey results, experimental data, and other forms of statistical information.
- Test scores: Standardized tests often report scores as percentages, indicating the proportion of correctly answered questions.
3. Science and Research
- Data representation: Scientists use percentages to represent proportions in various data sets and research findings.
- Experimental results: Analyzing the success rate of an experiment or the effectiveness of a treatment often involves percentage calculations.
- Statistical modeling: Percentages play a critical role in building statistical models and analyzing probabilities.
4. Everyday Life
- Tip calculations: Restaurants often expect tips calculated as a percentage of the total bill.
- Sales tax: Governments levy sales tax on goods and services, typically expressed as a percentage.
- Household budgeting: Individuals utilize percentages to track their spending across different budget categories.
Related Percentage Calculations: Expanding Your Knowledge
Understanding the calculation of "7 out of 18 as a percentage" provides a foundation for tackling other percentage-related problems. Here are some related calculations:
1. Calculating the Percentage Increase or Decrease
Percentage change is a common calculation used to express the relative change between two values. The formula is:
[(New Value - Old Value) / Old Value] × 100
For example, if sales increased from 100 to 120, the percentage increase is:
[(120 - 100) / 100] × 100 = 20%
2. Finding a Percentage of a Number
Calculating a percentage of a number is straightforward:
(Percentage / 100) × Number
For instance, to find 25% of 80:
(25 / 100) × 80 = 20
3. Determining the Original Value Given a Percentage Change
If you know the new value and the percentage change, you can find the original value using this formula:
Original Value = New Value / (1 + Percentage Change/100) (for percentage increase) Original Value = New Value / (1 - Percentage Change/100) (for percentage decrease)
For example, if the price increased by 10% to $110, the original price was:
$110 / (1 + 10/100) = $100
Advanced Concepts: Understanding the Limitations
While percentages are powerful tools, it's crucial to understand their limitations:
- Context is Key: A percentage alone lacks meaning without context. For example, a 10% increase in sales is significant for a small business but may be insignificant for a large corporation.
- Misleading Statistics: Percentages can be manipulated to create misleading impressions. Always critically analyze the data presented and consider the source.
- Large Numbers and Small Changes: Small percentage changes can represent substantial absolute changes when dealing with large numbers.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, specifically as illustrated by the example of "7 out of 18 as a percentage," is a crucial skill with widespread applications. This article has provided a step-by-step guide, explored related concepts, and highlighted the importance of context and critical analysis when interpreting percentage-based data. By mastering these concepts, you'll be better equipped to analyze information, make informed decisions, and communicate effectively across various contexts. Remember to always consider the context and potential limitations of percentages to ensure accurate and meaningful interpretations.
Latest Posts
Latest Posts
-
Which Of The Following Ratios Correctly Describes The Tangent Function
May 11, 2025
-
What Can You Do With A Cricket
May 11, 2025
-
What Coffee Has The Least Caffeine At Starbucks
May 11, 2025
-
What Is 3 4 Pound In Ounces
May 11, 2025
-
Is The Square Root Of 25 Irrational
May 11, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 18 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.