8.6 Rounded To The Nearest Whole Number
Arias News
Apr 05, 2025 · 6 min read
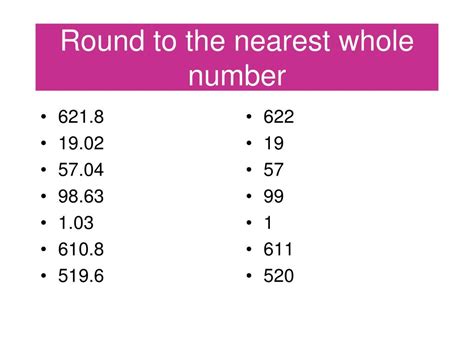
Table of Contents
8.6 Rounded to the Nearest Whole Number: A Comprehensive Guide
Rounding numbers is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating bills and budgeting to understanding scientific data and statistical analysis. This article delves into the process of rounding, focusing specifically on rounding 8.6 to the nearest whole number, while also providing a broader understanding of rounding techniques and their importance.
Understanding the Concept of Rounding
Rounding is a process of approximating a number to a specified level of precision. It involves simplifying a number by reducing the number of significant digits while maintaining a reasonable degree of accuracy. The result is a number that is easier to work with and understand, particularly when dealing with large datasets or numbers with many decimal places.
The core principle of rounding hinges on identifying the place value to which you're rounding. Commonly, we round to the nearest whole number (ones place), tenth, hundredth, or even thousandth. The decision of whether to round up or down depends on the digit immediately to the right of the specified place value.
The Rules of Rounding
The rules governing rounding are straightforward but crucial for accurate results. Here's a breakdown:
-
Identify the place value: Determine the place value to which you need to round. In our case, it's the ones place.
-
Look at the next digit: Examine the digit immediately to the right of the place value you've identified. For 8.6, this is the digit 6 (in the tenths place).
-
Apply the rule:
- If the digit is 5 or greater (5, 6, 7, 8, 9), round up: This means you increase the digit in the place value by 1.
- If the digit is less than 5 (0, 1, 2, 3, 4), round down: This means you leave the digit in the place value as it is. Digits to the right of the place value become 0.
Rounding 8.6 to the Nearest Whole Number: A Step-by-Step Approach
Let's apply these rules to round 8.6 to the nearest whole number:
-
Identify the place value: We need to round to the nearest whole number, which is the ones place.
-
Look at the next digit: The digit to the right of the ones place (8) is 6.
-
Apply the rule: Since 6 is greater than or equal to 5, we round up. This means we increase the digit in the ones place (8) by 1.
-
The result: Therefore, 8.6 rounded to the nearest whole number is 9.
Practical Applications of Rounding
Rounding finds applications across various fields:
-
Finance: Rounding is essential in calculating taxes, interest rates, and currency conversions. For example, a bank might round transaction amounts to the nearest cent.
-
Science: Scientific measurements often involve rounding to reflect the accuracy of the measuring instrument. A scientist might round a measurement of 12.456 cm to 12.5 cm for simplicity and to avoid suggesting a higher level of accuracy than achievable.
-
Engineering: Rounding is crucial in engineering designs and calculations where precise dimensions are paramount. However, rounding may be necessary to simplify calculations or conform to available materials.
-
Statistics: Rounding is used extensively in statistical analysis, summarizing large datasets, and presenting results in a clear and concise manner. Averages or means might be rounded to a certain number of decimal places for ease of interpretation.
-
Everyday Life: We use rounding unconsciously in everyday scenarios, like estimating the total cost of groceries or calculating tips in restaurants.
Significance of Rounding in Data Analysis and Presentation
Rounding plays a crucial role in data analysis and presentation, contributing significantly to the clarity and readability of results. It simplifies complex datasets, making them easier to interpret and understand.
When presenting data, rounding helps to avoid overwhelming the audience with excessive precision. For instance, a report on population figures might round population numbers to the nearest thousand to avoid unnecessary detail. However, it's important to be mindful of the potential for introducing errors due to repeated rounding. Always maintain a clear record of the original, unrounded data for future analysis and calculations.
Advanced Rounding Techniques: Rounding Rules for 5
A common question arises regarding rounding when the digit to the right of the rounding place is exactly 5. There are different approaches to this, and the best method depends on the context and desired level of accuracy.
One method is to consistently round up if the digit is 5. Another, often preferred in scientific contexts, is to round to the nearest even number. This method helps to reduce bias over many rounding operations. For example, 2.5 would round to 2, while 3.5 would round to 4. This "round to even" or "banker's rounding" method minimizes cumulative error over many calculations.
Errors Introduced by Rounding: Significant Figures and Precision
While rounding simplifies data, it's essential to acknowledge the inherent error introduced. Understanding significant figures is crucial in this regard. Significant figures represent the number of digits that carry meaning contributing to the precision of a measurement. Rounding reduces the number of significant figures, impacting the overall precision.
It's important to balance simplification with accuracy. Overly aggressive rounding can lead to substantial errors, especially in cumulative calculations. Choosing the appropriate level of precision is essential, depending on the context and acceptable margin of error.
Alternatives to Rounding: Truncation and Floor/Ceiling Functions
Besides rounding, there are other methods of approximating numbers:
-
Truncation: This involves simply removing the digits to the right of the specified place value. For instance, truncating 8.6 to the nearest whole number would result in 8. This method is less common than rounding because it introduces a systematic bias.
-
Floor and ceiling functions: These functions always round down (floor) or up (ceiling) respectively, regardless of the value of the digit to the right. These functions are useful in specific programming and mathematical contexts but are less commonly used in everyday applications.
Conclusion: The Importance of Understanding Rounding
Rounding numbers is a fundamental mathematical skill with far-reaching implications across numerous disciplines. Understanding the basic rules of rounding, particularly the distinctions between rounding up and down, and considering more sophisticated methods like rounding to even, allows for effective data analysis, presentation, and problem-solving in everyday situations. The key is to balance simplification with accuracy, recognizing the potential for error and choosing the most appropriate method for a given context. By mastering these concepts, you can confidently navigate numerical computations and enhance your understanding of mathematical applications in the real world. Remember that the seemingly simple act of rounding plays a critical role in ensuring clarity, precision, and effective communication of numerical information.
Latest Posts
Latest Posts
-
John Deere Oil Filter Am125424 Cross Reference Chart
Apr 05, 2025
-
How Is Grendel Characterized In This Excerpt
Apr 05, 2025
-
I Was Born In 1971 How Old Am I
Apr 05, 2025
-
How Tall Is 82 Inches In Feet
Apr 05, 2025
-
Which Statement Best Illustrates An Example Of Economic Specialization
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about 8.6 Rounded To The Nearest Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
