8 Thousandths + 6 Ones 8 Thousandths
Arias News
May 10, 2025 · 5 min read
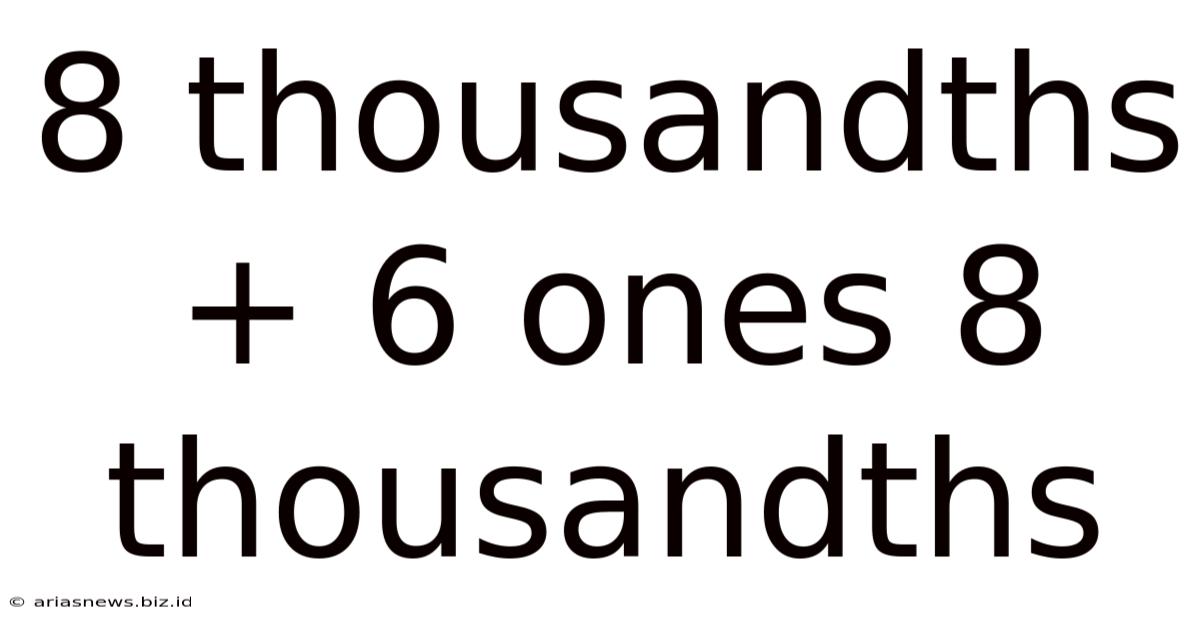
Table of Contents
8 Thousandths + 6 Ones 8 Thousandths: A Deep Dive into Decimal Addition
This article explores the seemingly simple addition problem of 8 thousandths + 6 ones 8 thousandths, delving far beyond the basic arithmetic to illuminate underlying mathematical concepts, explore diverse application scenarios, and provide practical strategies for solving similar problems. We’ll examine the problem's structure, discuss different methods of solution, and highlight the importance of understanding decimal place value in various real-world contexts.
Understanding Decimal Place Value: The Foundation of the Problem
Before we tackle the addition, it's crucial to grasp the concept of decimal place value. Our number system is based on powers of ten. Each position to the left of the decimal point represents a progressively larger power of ten (ones, tens, hundreds, etc.), while each position to the right represents a progressively smaller fraction of ten (tenths, hundredths, thousandths, etc.).
Understanding the Numbers:
-
8 thousandths: This is written as 0.008. The 8 is in the thousandths place, meaning it represents 8/1000.
-
6 ones 8 thousandths: This is written as 6.008. The 6 is in the ones place, representing 6 whole units. The .008 represents 8 thousandths, as explained above.
Understanding place value is fundamental not just for adding decimals but also for all arithmetic operations involving decimal numbers, including subtraction, multiplication, and division. A firm grasp of this concept prevents common errors and enables accurate calculations.
Method 1: Direct Addition Using Columns
This is the most straightforward method. We align the decimal points vertically and add the numbers column by column, carrying over when necessary.
6.008
+ 0.008
-------
6.016
Adding the thousandths column (8 + 8 = 16), we carry-over the 1 to the hundredths column. The hundredths column now becomes 1 (carried over) + 0 + 0 = 1. The tenths column remains 0, and the ones column remains 6. Therefore, the sum is 6.016.
Method 2: Converting to Fractions
We can convert the decimals to fractions to perform the addition. This method reinforces the understanding of decimal representation.
-
8 thousandths: 8/1000
-
6 ones 8 thousandths: 6 + 8/1000 = 6000/1000 + 8/1000 = 6008/1000
Adding the fractions:
6008/1000 + 8/1000 = 6016/1000
Converting this fraction back to a decimal:
6016/1000 = 6.016
Method 3: Using a Number Line
While less efficient for this specific problem, visualizing the addition on a number line can be helpful for understanding the concept, especially when working with larger numbers or more complex decimal additions. You would start at 6.008 and move 0.008 units to the right.
Real-World Applications: Where This Type of Calculation Matters
The seemingly simple addition of 8 thousandths and 6 ones 8 thousandths has numerous real-world applications across various fields.
1. Finance and Accounting:
-
Calculating interest: Compound interest calculations often involve adding small decimal amounts representing interest earned over time.
-
Tracking expenses: Balancing budgets requires adding various expenses, often expressed as decimals (e.g., $6.008 for groceries and $0.008 for a small item).
-
Currency conversions: Converting currencies often involves working with decimals representing exchange rates.
2. Science and Engineering:
-
Measurements: Scientific measurements frequently involve decimal values. Adding small increments is crucial in experiments or engineering projects. For example, adding the small change in a measured variable.
-
Data analysis: Analyzing data sets often requires performing calculations with decimal numbers, such as averaging or calculating standard deviations.
3. Everyday Life:
-
Shopping: Calculating the total cost of items with prices including cents (e.g., $6.08 and $0.08).
-
Cooking and baking: Measuring ingredients accurately often involves working with fractions and decimals that require adding or subtracting amounts.
Error Prevention and Best Practices
Several strategies can help prevent common errors when working with decimal addition:
-
Careful alignment: Always ensure that the decimal points are aligned vertically before adding. This is crucial for accurate placement of digits.
-
Place value understanding: A strong understanding of place value is fundamental to performing decimal operations correctly.
-
Estimation: Before performing the calculation, estimate the result. This helps to identify potential errors. For instance, we know 6.008 + 0.008 should be slightly more than 6.
-
Check your work: After completing the addition, review the steps and check for any mistakes.
Extending the Concept: More Complex Decimal Additions
While this article focuses on a relatively simple example, the principles discussed are applicable to more complex decimal additions. For instance:
-
Adding multiple decimals: The same techniques can be applied to adding three or more decimal numbers.
-
Adding decimals with differing numbers of decimal places: When adding decimals with different numbers of decimal places, it's helpful to add trailing zeros to the shorter numbers to ensure consistent alignment. For example, adding 6.008 and 0.5 would involve rewriting 0.5 as 0.500 for easier addition.
-
Adding decimals and whole numbers: Combining whole numbers with decimals is essentially the same process.
Conclusion: Mastering Decimal Addition for a Stronger Mathematical Foundation
Mastering decimal addition is not just about getting the right answer; it's about cultivating a deeper understanding of our number system and its practical applications. This article has detailed a seemingly simple problem, but the underlying principles are critical for success in various academic and professional contexts. By understanding place value, employing different calculation methods, and implementing error prevention strategies, one can build a strong foundation in decimal arithmetic and apply this knowledge to a wide range of real-world scenarios. The ability to perform accurate and efficient decimal calculations is an invaluable skill for anyone navigating the complexities of the modern world.
Latest Posts
Latest Posts
-
Where To Buy Bose Radio Cd Player
May 10, 2025
-
Which Of The Following Descriptions Matches The Balance Exercise Principle
May 10, 2025
-
Why Did Zorna Pour Ketchup On Her Brothers Hands
May 10, 2025
-
Average Iq For An 11 Year Old
May 10, 2025
-
A Hexagon With Exactly 1 Pair Of Perpendicular Sides
May 10, 2025
Related Post
Thank you for visiting our website which covers about 8 Thousandths + 6 Ones 8 Thousandths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.