Blank Plus Blank Plus Blank Equals 30
Arias News
May 12, 2025 · 5 min read
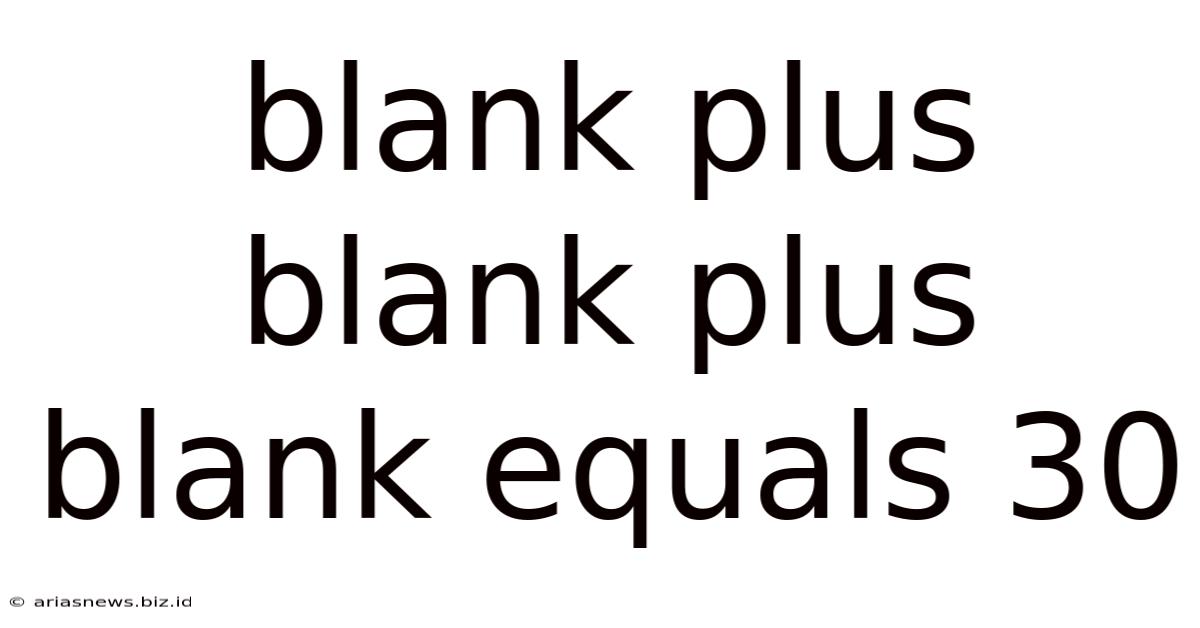
Table of Contents
Blank Plus Blank Plus Blank Equals 30: Unraveling the Mathematical Puzzle and Exploring Creative Solutions
The deceptively simple equation, "Blank + Blank + Blank = 30," presents a captivating mathematical puzzle that sparks curiosity and invites creative problem-solving. While seemingly straightforward, the challenge lies in the limitations imposed: the blanks can only be filled with single-digit numbers (0-9) and each blank must represent a distinct number. This seemingly simple constraint opens a world of possibilities and introduces important mathematical and logical concepts. This article will delve into various approaches to solving this puzzle, exploring different mathematical strategies, highlighting the importance of logical reasoning, and even venturing into more creative interpretations.
Understanding the Problem: Constraints and Possibilities
At the heart of this puzzle is the constraint that each blank must contain a unique single-digit number. This immediately limits the potential combinations significantly. We’re not dealing with an infinite number of possibilities; instead, we're working with a finite set, making systematic exploration feasible. Let's break down the core challenge:
- Uniqueness: Each blank must contain a different digit (0-9). This means repetition is prohibited.
- Sum: The sum of the three unique digits must equal 30.
- Single Digits: The numbers used are limited to the digits 0 through 9.
This seemingly simple constraint transforms the problem into a captivating mathematical exercise requiring both logical deduction and a bit of trial-and-error.
Methodical Approach: Systematic Elimination and Trial and Error
One effective approach is to employ a systematic method involving trial and error combined with logical elimination. We can start by identifying the largest possible numbers that can be used. If we choose 9, 8, and 7, the sum is 24, falling short of the target 30. However, this gives us a valuable starting point: We need larger numbers to approach the target sum.
Let's try a different combination. If we select 9, 8, and 7, the sum is 24. That’s too low. Let's try higher numbers:
- Trying larger numbers: If we choose the highest three numbers (9, 8, and 7), the sum is only 24. This immediately tells us that we need to explore combinations that include numbers greater than 7 to reach 30.
- Eliminating impossible combinations: We can systematically eliminate combinations that will clearly not work. For instance, if we choose 1, 2, and 3, we're far too low. This strategy involves a systematic process of trial and error, guided by logical deduction.
- Focusing on the high end: It’s more efficient to start with larger numbers and work our way down, as this will quickly reveal if high-number combinations are impossible.
Through this trial-and-error approach, coupled with eliminating clearly impossible combinations, you will eventually stumble upon the solution.
Exploring the Solution: The Significance of Logical Reasoning
The solution to the puzzle isn't necessarily unique in the sense that it may involve more than one possible mathematical pathway to the answer, demonstrating that multiple valid solutions might exist. This highlights the importance of logical reasoning and careful methodical consideration of different permutations rather than relying solely on trial and error.
Beyond the Numbers: Expanding the Problem’s Scope
The seemingly simple mathematical puzzle of "Blank + Blank + Blank = 30" extends beyond its immediate mathematical context. It offers opportunities to explore several interconnected concepts:
1. Combinatorics and Permutations:
The puzzle naturally leads into the study of combinatorics and permutations. It encourages exploration of the various possible combinations of three distinct digits from 0 to 9. This provides a concrete example of counting principles in action. Exploring how many possible combinations exist before applying the constraint that the sum must be 30 is an excellent exercise.
2. Problem-Solving Strategies:
This puzzle exemplifies the effectiveness of different problem-solving strategies, including:
- Trial and Error: A straightforward method, but more efficient when combined with logical elimination.
- Systematic Elimination: Identifying and discarding combinations that are clearly impossible.
- Logical Deduction: Using prior results to guide subsequent attempts.
3. Critical Thinking and Pattern Recognition:
The puzzle fosters critical thinking skills by encouraging the identification of patterns and relationships among numbers. Successfully solving the puzzle often involves recognizing the relationships between different combinations and how they contribute to or detract from the target sum of 30.
4. Algorithmic Thinking:
For more advanced problem-solvers, the puzzle could inspire the creation of an algorithm to systematically test all possible combinations of three unique digits and identify those that sum to 30. This might involve programming in Python or other programming languages, translating the logical thought process into a set of computational steps.
Creative Interpretations and Extensions
The core concept can be extended and adapted in various ways, enhancing its educational and entertainment value:
- Different Target Sums: Instead of 30, we could use any other target sum. This introduces additional layers of complexity and provides practice in adjusting strategies.
- More Blanks: Adding more blanks increases the complexity exponentially, requiring more sophisticated approaches to solving the problem.
- Using Operations: Instead of simply addition, we could introduce other operations like subtraction, multiplication, and division, leading to completely new sets of solutions and requiring significantly more complex problem-solving strategies.
- Using Negative Numbers: This could make the puzzle far more intricate, extending into potentially an infinite number of solutions.
Conclusion: More Than Just a Math Puzzle
The seemingly simple equation "Blank + Blank + Blank = 30" proves to be far more enriching than its initial appearance suggests. It seamlessly integrates mathematical concepts with logical reasoning, problem-solving strategies, and critical thinking skills. Furthermore, it extends naturally into creative exploration and algorithmic thinking. This simple puzzle serves as a compelling illustration of how seemingly straightforward problems can lead to deeper mathematical insights and broaden our problem-solving capabilities. The puzzle's enduring appeal lies in its ability to challenge and engage individuals of varying mathematical backgrounds, offering a stimulating intellectual exercise for all.
Latest Posts
Related Post
Thank you for visiting our website which covers about Blank Plus Blank Plus Blank Equals 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.