Can A Number Be Both Rational And Irrational
Arias News
Apr 03, 2025 · 5 min read
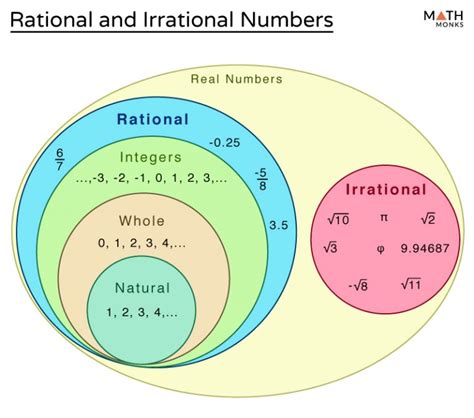
Table of Contents
Can a Number Be Both Rational and Irrational? A Deep Dive into Number Systems
The question, "Can a number be both rational and irrational?" might seem trivial at first glance. The answer, unequivocally, is no. However, understanding why this is the case requires a deeper exploration of the fundamental definitions and properties of rational and irrational numbers. This article will delve into the intricacies of number systems, clarifying the distinct characteristics of rational and irrational numbers and explaining why their intersection is an empty set. We'll explore examples, delve into proofs, and consider common misconceptions surrounding these concepts.
Understanding Rational Numbers
A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. This seemingly simple definition has profound implications. Let's break it down:
- Integers: Integers encompass whole numbers (positive, negative, and zero). Examples include -3, 0, 5, 100, etc.
- Fraction: The fraction representation is key. It means that every rational number can be written as a ratio of two whole numbers.
- q ≠ 0: This crucial condition prevents division by zero, an undefined operation in mathematics.
Examples of Rational Numbers:
- 1/2: A simple fraction.
- -3/4: A negative fraction.
- 5: Can be expressed as 5/1. All integers are rational numbers.
- 0.75: Can be expressed as 3/4. Terminating decimals are rational.
- 0.333... (repeating decimal): Can be expressed as 1/3. Repeating decimals are also rational.
Understanding Irrational Numbers
Irrational numbers, in contrast, cannot be expressed as a fraction of two integers. This seemingly simple difference leads to significant mathematical consequences. The defining characteristic of irrational numbers is their non-terminating and non-repeating decimal representation.
This means that their decimal expansion goes on forever without ever settling into a repeating pattern. Trying to write them as a fraction will always fail.
Examples of Irrational Numbers:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... Its decimal expansion continues infinitely without repeating.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828... Another non-repeating, infinite decimal.
- √2 (square root of 2): This number, approximately 1.41421..., cannot be expressed as a fraction of two integers. This can be proven using proof by contradiction (more on this later).
- The golden ratio (φ): Approximately 1.61803..., also known as the divine proportion, is an irrational number with fascinating mathematical properties.
The Mutually Exclusive Nature of Rational and Irrational Numbers
The key to understanding why a number cannot be both rational and irrational lies in their fundamentally opposing definitions. A number is either expressible as a fraction of two integers (rational) or it is not (irrational). There is no middle ground.
Imagine a Venn diagram representing rational and irrational numbers. These two sets are disjoint, meaning they share no common elements. Their intersection is an empty set. This fundamental incompatibility prevents any number from simultaneously belonging to both categories.
Proof by Contradiction: The Case of √2
A classic example illustrating the mutual exclusivity is the proof that √2 is irrational. This proof uses a method called "proof by contradiction":
-
Assumption: Let's assume, for the sake of contradiction, that √2 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q have no common factors other than 1).
-
Squaring both sides: If √2 = p/q, then squaring both sides gives 2 = p²/q².
-
Rearranging: This can be rearranged to 2q² = p². This equation tells us that p² is an even number (because it's equal to 2 times another integer).
-
Implication: If p² is even, then p must also be even (because the square of an odd number is always odd). This means we can express p as 2k, where k is another integer.
-
Substitution: Substituting p = 2k into the equation 2q² = p², we get 2q² = (2k)² = 4k².
-
Simplifying: Dividing both sides by 2 gives q² = 2k². This shows that q² is also an even number, and therefore q must be even.
-
Contradiction: We've now shown that both p and q are even numbers. This contradicts our initial assumption that the fraction p/q was in its simplest form (they should have no common factors other than 1).
-
Conclusion: Since our initial assumption leads to a contradiction, the assumption must be false. Therefore, √2 cannot be expressed as a fraction of two integers, meaning it is irrational.
Common Misconceptions
Several misconceptions surround rational and irrational numbers:
- Non-terminating decimals are always irrational: This is false. Repeating decimals, like 0.333..., are rational. It's the non-repeating nature that makes a decimal irrational.
- Irrational numbers are somehow "less real": Both rational and irrational numbers are equally valid and essential components of the real number system. They are not different in their existence or "reality."
- Approximations are the same as the exact value: Approximations of irrational numbers (like using 3.14 for π) are useful in practical calculations, but they are not the same as the exact, infinite value of the irrational number itself.
The Real Number System: A Unified Whole
Rational and irrational numbers together form the set of real numbers. The real number system encompasses all numbers that can be plotted on a number line. Understanding the distinctions between rational and irrational numbers is crucial for a complete understanding of real analysis, calculus, and many other advanced mathematical concepts. While they are distinct subsets, they are essential parts of a comprehensive and unified mathematical framework.
Conclusion
The answer to the question, "Can a number be both rational and irrational?" is a definitive no. Their definitions are mutually exclusive. A number is either expressible as a fraction of two integers or it is not. The proof surrounding the irrationality of √2 serves as a powerful example of the elegance and rigor of mathematical reasoning. A firm grasp of the properties and distinctions between rational and irrational numbers is fundamental to a deep understanding of mathematics and its applications. Their coexistence within the real number system underscores the richness and complexity of the mathematical landscape.
Latest Posts
Latest Posts
-
If Born In 1991 How Old Are You
Apr 04, 2025
-
How To Know If Zucchini Is Bad
Apr 04, 2025
-
What Percentage Is 11 Out Of 14
Apr 04, 2025
-
How Many Hours Is 8am To 7pm
Apr 04, 2025
-
How Many Square Feet Is 22 Acres
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Can A Number Be Both Rational And Irrational . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
