Divide 20 By Half And Add 30
Arias News
May 09, 2025 · 5 min read
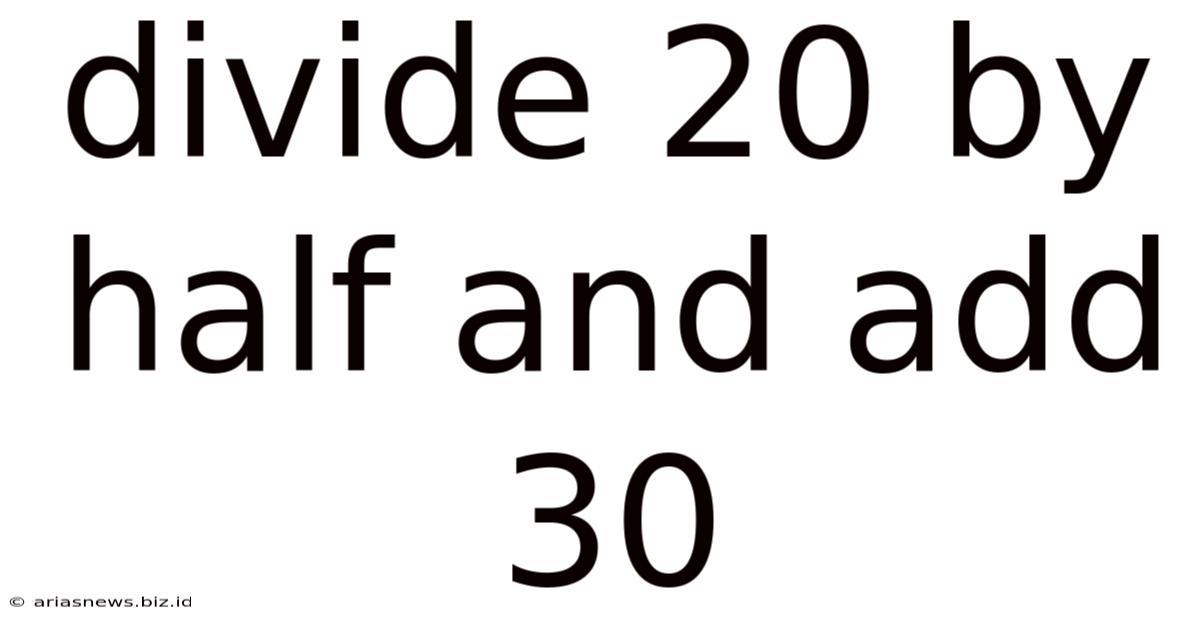
Table of Contents
Divide 20 by Half and Add 30: A Deep Dive into a Simple Math Problem
This seemingly simple math problem, "Divide 20 by half and add 30," is a classic example of how phrasing can dramatically alter the outcome. It's a fun little brain teaser that highlights the importance of precise language in mathematics and problem-solving. This article will not only solve the problem but also explore its underlying mathematical concepts, variations, and applications in a broader context. We'll delve into why this question is more than just a simple arithmetic exercise and examine its value in teaching critical thinking skills.
Understanding the Ambiguity: The Power of Language
The core reason this problem is intriguing is its ambiguity. The phrase "divide 20 by half" can be interpreted in two distinct ways:
-
Interpretation 1: Divide 20 by 1/2: This interpretation involves dividing 20 by the fraction 1/2. In mathematical terms, this is equivalent to multiplying 20 by the reciprocal of 1/2, which is 2. Therefore, 20 divided by 1/2 is 20 * 2 = 40. Adding 30 to this result gives us 40 + 30 = 70.
-
Interpretation 2: Divide 20 by 2: This interpretation involves dividing 20 by the number 2, which is a much simpler calculation. 20 / 2 = 10. Adding 30 yields 10 + 30 = 40.
The Solution: Two Answers, One Problem
The beauty (and the challenge) of this problem lies in the fact that it has two valid answers, depending on how one interprets the wording. This highlights the importance of clear and unambiguous language, especially in mathematical contexts. Without precise instruction, the problem is open to multiple interpretations, leading to different solutions.
Therefore, the answer to "Divide 20 by half and add 30" is either 70 or 40, depending on the interpretation.
Beyond the Numbers: Exploring Mathematical Concepts
While seemingly trivial, this problem touches upon several crucial mathematical concepts:
1. Fractions and Reciprocals:
The first interpretation directly involves working with fractions. Dividing by a fraction is equivalent to multiplying by its reciprocal. This highlights a fundamental rule in arithmetic operations. Understanding reciprocals is essential for various mathematical procedures, including solving equations, simplifying expressions, and working with ratios and proportions.
2. Order of Operations (PEMDAS/BODMAS):
While this specific problem doesn't heavily rely on strict adherence to the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), it underscores the importance of considering the order of operations in more complex calculations. The ambiguity in the question stems from the lack of explicit parentheses or clear ordering, thereby affecting the interpretation and subsequent solution.
3. Ambiguity and Precision in Language:
The problem serves as a powerful reminder of how important clear and unambiguous communication is in mathematics and beyond. Vague language can lead to misunderstandings and incorrect conclusions. This is crucial in fields ranging from engineering and finance to software development, where precise instructions are paramount.
Practical Applications and Real-World Scenarios
While this may seem like a purely academic exercise, understanding the underlying principles has real-world applications:
1. Data Analysis and Interpretation:
Interpreting data often involves calculations similar to this problem. Misunderstanding the language used to describe a statistical process can lead to incorrect analysis and conclusions. For example, interpreting data related to percentages, ratios, and rates requires careful attention to detail and a clear understanding of the underlying mathematical operations.
2. Software Development and Programming:
In computer programming, the order of operations and precise syntax are critical. A misplaced operator or an unclear instruction can lead to program errors and unexpected outcomes. Similar to the ambiguity in our problem, even small inaccuracies in code can have significant consequences.
3. Financial Calculations:
Financial calculations, such as calculating interest rates or investment returns, require precision and clarity. Incorrect interpretation of financial statements or formulas can lead to serious errors in budgeting, investing, and financial planning. The ability to accurately interpret financial language is key to making sound financial decisions.
Variations and Extensions
The problem's simplicity allows for easy variations and extensions:
-
Increased Complexity: We could increase the complexity by adding more operations or using more complex numbers, such as decimals or fractions. This would challenge students to further refine their understanding of order of operations and fraction manipulation.
-
Word Problems: The problem can be framed as a word problem, requiring students to translate the words into mathematical expressions. This helps develop problem-solving skills and enhances their ability to translate real-world scenarios into mathematical models.
-
Algebraic Representation: The problem can be represented algebraically, for example: (20 ÷ x) + 30 = y, where x can be 1/2 or 2 and solving for y. This helps students transition from arithmetic to more advanced algebraic thinking.
Teaching Critical Thinking: More Than Just Math
This problem is an excellent tool for teaching critical thinking skills:
-
Identifying Ambiguity: Students learn to identify ambiguous language and interpret multiple meanings, which is a crucial skill applicable in various fields.
-
Logical Reasoning: The problem prompts students to use logical reasoning to analyze the problem and arrive at the correct solution, regardless of the interpretation.
-
Precise Communication: The problem emphasizes the need for precise communication in mathematical settings. Students learn to appreciate the importance of clear and unambiguous language.
-
Problem-Solving Strategies: Students develop various problem-solving strategies by considering different interpretations and evaluating their validity.
Conclusion: A Simple Problem with Profound Implications
The seemingly simple problem, "Divide 20 by half and add 30," is a surprisingly rich mathematical puzzle. Its ambiguity highlights the importance of clear communication and precise language in mathematical contexts. By analyzing its different interpretations and the underlying mathematical concepts, we gain a deeper understanding of the importance of clear instructions, fraction manipulation, and the order of operations. Beyond its immediate mathematical value, this problem serves as an engaging tool for teaching critical thinking skills and developing robust problem-solving strategies. It reminds us that even the simplest problems can hold significant lessons, encouraging us to think critically and precisely, whether we are dealing with numbers or words. This problem's ability to spark discussion and critical thought makes it far more valuable than a simple arithmetic exercise.
Latest Posts
Latest Posts
-
How Much Protein Is In Three Scrambled Eggs
May 09, 2025
-
Can You Eat Grits On The Daniel Fast
May 09, 2025
-
What Percentage Is 44 Out Of 60
May 09, 2025
-
What Is The Shortest Book In The Old Testament
May 09, 2025
-
What Does In Launcher Mean In Fortnite
May 09, 2025
Related Post
Thank you for visiting our website which covers about Divide 20 By Half And Add 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.