Do The Diagonals Of A Kite Bisect Bisect The Angles
Arias News
Apr 02, 2025 · 5 min read
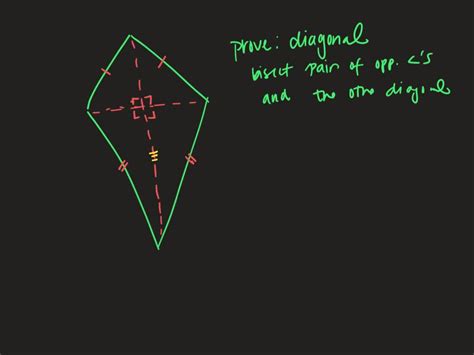
Table of Contents
Do the Diagonals of a Kite Bisect the Angles? Exploring the Geometry of Kites
The question of whether the diagonals of a kite bisect its angles is a fundamental concept in geometry, often explored in middle and high school mathematics. While the answer might seem straightforward at first glance, a deeper understanding requires a careful examination of the kite's properties and the definition of angle bisection. This article will delve into the intricacies of kite geometry, proving which angles are bisected and why, and clarifying common misconceptions. We'll explore different approaches, from geometric proofs to visual representations, to solidify your grasp of this important concept.
Understanding the Properties of a Kite
Before we dive into the angle bisector question, let's establish a firm understanding of what defines a kite. A kite is a quadrilateral – a four-sided polygon – with two pairs of adjacent sides that are congruent. This means that two sides sharing a vertex have equal lengths. Critically, these congruent sides are adjacent, not opposite. This characteristic distinguishes a kite from a parallelogram or a rhombus.
Here's a breakdown of the key properties of a kite:
- Two pairs of adjacent congruent sides: This is the defining characteristic of a kite.
- One pair of opposite angles are congruent: The angles between the pairs of congruent sides are equal.
- Diagonals are perpendicular: The lines connecting opposite vertices intersect at a right angle (90 degrees).
- One diagonal bisects the other: One diagonal is divided into two equal segments by the other. Importantly, this is not always true for both diagonals.
It is this final point, along with the perpendicularity of the diagonals, which forms the basis of our investigation into angle bisection.
Do the Diagonals Always Bisect the Angles? A Definitive Answer
The short answer is: no, the diagonals of a kite do not always bisect its angles. Only one diagonal consistently bisects the angles, and that's the diagonal that connects the vertices where the pairs of congruent sides meet. Let's break this down:
-
The diagonal connecting the vertices of the congruent sides bisects the angles at those vertices: This is a crucial property. This diagonal acts as an axis of symmetry, dividing the kite into two congruent triangles. Because of this symmetry, the angles on either side of this diagonal are equal, meaning the diagonal bisects them.
-
The other diagonal does not bisect the angles: This diagonal connects the vertices of the non-congruent sides. Unless the kite is also a rhombus (where all four sides are equal), this diagonal will not bisect the angles at either end. This is because the triangles formed on either side of this diagonal are not congruent.
Visualizing the Concept: A Diagrammatic Approach
Imagine a kite ABCD, where AB = BC and CD = DA. Let's label the intersection of the diagonals as point O.
[Imagine a diagram here showing kite ABCD with diagonals AC and BD intersecting at point O. AC bisects angles A and C. BD does not bisect angles B and D.]
In this diagram, diagonal AC (the one connecting the vertices of congruent sides) bisects angles ∠BAC and ∠DCA, resulting in ∠BAO = ∠CAO and ∠DCO = ∠ACO. However, diagonal BD does not bisect angles ∠ABD and ∠CBD, nor angles ∠ADB and ∠CDB, unless the kite is a special case, such as a rhombus (which is a special type of kite where all four sides are equal).
Geometric Proof: Dissecting the Angle Bisection
Let's formally prove that the diagonal connecting the vertices of the congruent sides bisects the angles at those vertices. We'll use a proof by congruence.
Given: Kite ABCD with AB = BC and CD = DA. Diagonal AC connects vertices A and C.
To Prove: ∠BAC = ∠DAC and ∠BCA = ∠DCA
Proof:
-
Consider triangles ΔABC and ΔADC: These triangles share the side AC.
-
AB = BC (Given): This is a property of the kite.
-
CD = DA (Given): This is also a property of the kite.
-
AC = AC (Reflexive Property): A side is congruent to itself.
-
ΔABC ≅ ΔADC (SSS Congruence): All three sides of ΔABC are congruent to the corresponding sides of ΔADC.
-
∠BAC = ∠DAC (CPCTC): Corresponding parts of congruent triangles are congruent. Therefore, diagonal AC bisects ∠A.
-
∠BCA = ∠DCA (CPCTC): Similarly, diagonal AC bisects ∠C.
This proof conclusively demonstrates that the diagonal connecting the vertices of the congruent sides bisects the angles at those vertices. This is a cornerstone property of kites.
Special Cases: When Both Diagonals Bisect Angles
While the general rule is that only one diagonal bisects the angles, there are specific situations where both diagonals bisect the angles. This occurs when the kite is also a rhombus. A rhombus is a quadrilateral with all four sides of equal length. Since a rhombus is a type of kite, it inherits all the properties of a kite, including the perpendicularity of its diagonals.
In a rhombus, the diagonals bisect each other and also bisect the angles. This is because a rhombus possesses additional symmetry compared to a general kite. The symmetry ensures that all four triangles formed by the diagonals are congruent.
Applications and Real-World Examples
Understanding the angle bisecting properties of a kite is not just an abstract geometric exercise. It has practical applications in various fields:
-
Engineering: Kite-shaped structures are sometimes used in construction and engineering, and understanding their geometric properties is essential for stability and design calculations.
-
Architecture: The symmetrical properties of kites can inspire architectural designs, contributing to aesthetically pleasing and structurally sound buildings.
-
Art and Design: The unique shape of a kite is often used in artistic creations and designs, including logos, patterns, and even kite-flying itself!
-
Computer Graphics: Understanding kite geometry is important in computer graphics for creating and manipulating shapes and polygons.
Conclusion: A Clearer Picture of Kite Geometry
The diagonals of a kite do not always bisect the angles. Only the diagonal connecting the vertices of the congruent sides consistently bisects the angles at those vertices. The other diagonal only bisects the angles in the special case where the kite is also a rhombus. Understanding this distinction requires a solid grasp of kite properties and geometric proofs. This exploration has provided a thorough analysis, incorporating visual aids and formal proof to solidify your comprehension of this fundamental geometric concept. Remember that mastering these geometrical concepts is vital for success in higher-level mathematics and its applications across various disciplines.
Latest Posts
Latest Posts
-
Which Italian Insects Often Fall In Love
Apr 03, 2025
-
Solve This Equation Y 9 5 0
Apr 03, 2025
-
3 Divided By 7 As A Fraction
Apr 03, 2025
-
How Many Hours Are In 100 Years
Apr 03, 2025
-
88 Cubic Inches Is How Many Cc
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Do The Diagonals Of A Kite Bisect Bisect The Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
