Do Two 1 3 Cups Equal 2 3
Arias News
May 08, 2025 · 5 min read
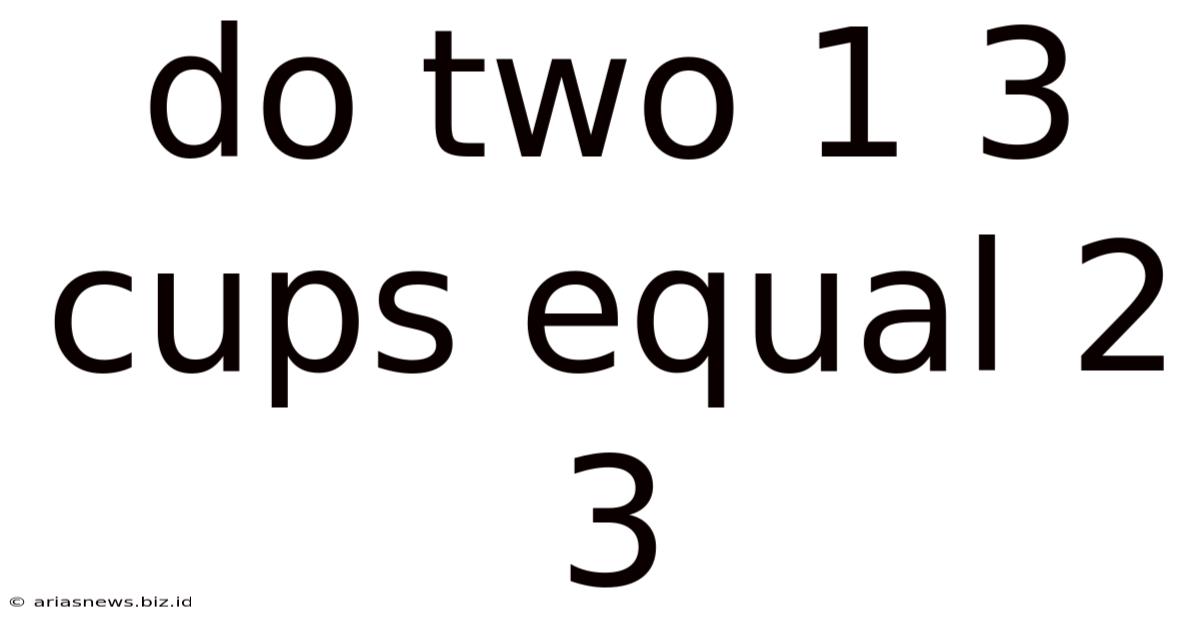
Table of Contents
Do Two 1⅓ Cups Equal 2⅔? Unpacking Fraction Math in Cooking and Beyond
Understanding fractions is crucial in many aspects of life, from baking a perfect cake to calculating financial investments. A common point of confusion, especially in culinary settings, involves adding mixed numbers – numbers that combine a whole number and a fraction. This article will delve into the question, "Do two 1⅓ cups equal 2⅔ cups?", providing a comprehensive explanation, exploring the mathematical principles involved, and offering practical applications to ensure a solid grasp of this concept.
Understanding Fractions: A Quick Refresher
Before tackling the main question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction ⅓, the numerator is 1, and the denominator is 3. This means we have one part out of three equal parts.
Mixed Numbers vs. Improper Fractions:
A mixed number, like 1⅓, combines a whole number (1 in this case) and a fraction (⅓). An improper fraction, on the other hand, has a numerator larger than or equal to its denominator (e.g., 4/3). It represents a value greater than or equal to one.
It's often helpful to convert between mixed numbers and improper fractions. To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator.
- Add the result to the numerator.
- Keep the same denominator.
For example, converting 1⅓ to an improper fraction:
- (1 x 3) = 3
- 3 + 1 = 4
- The improper fraction is 4/3.
Conversely, to convert an improper fraction to a mixed number:
- Divide the numerator by the denominator.
- The quotient becomes the whole number.
- The remainder becomes the numerator of the new fraction.
- The denominator remains the same.
For example, converting 4/3 to a mixed number:
- 4 ÷ 3 = 1 with a remainder of 1.
- The whole number is 1.
- The remainder is 1, so the numerator is 1.
- The denominator is 3.
- The mixed number is 1⅓.
Addressing the Central Question: Do Two 1⅓ Cups Equal 2⅔ Cups?
Now, let's address the central question: do two 1⅓ cups equal 2⅔ cups? The answer is no. Let's understand why.
We need to add two instances of 1⅓ cups. We can do this in two ways:
Method 1: Using Improper Fractions:
- Convert 1⅓ to an improper fraction: 4/3
- Add the two fractions: (4/3) + (4/3) = 8/3
- Convert the improper fraction 8/3 back to a mixed number: 8 ÷ 3 = 2 with a remainder of 2. Therefore, 8/3 = 2⅔ cups.
Method 2: Using Mixed Numbers:
- Add the whole numbers: 1 + 1 = 2
- Add the fractions: ⅓ + ⅓ = ⅔
- Combine the whole number and fraction: 2⅔ cups.
Both methods clearly demonstrate that two 1⅓ cups equal 2⅔ cups, not 2⅔ cups. The initial statement is therefore incorrect.
Common Mistakes and Misconceptions
One common mistake is adding the whole numbers and the fractions separately without considering the overall value. Someone might incorrectly think: 1 + 1 = 2 and ⅓ + ⅓ = ⅔, but then incorrectly combine them as 2⅓ instead of the correct 2⅔. This highlights the importance of understanding how to correctly work with mixed numbers.
Practical Applications: Cooking and Beyond
The ability to accurately add fractions is essential in various contexts. Here are a few examples:
-
Baking and Cooking: Recipes often require precise measurements. If a recipe calls for 1⅓ cups of flour in two different steps, accurately calculating the total amount of flour needed is crucial for successful baking.
-
Construction and Engineering: Accurate measurements are vital in construction and engineering projects. Miscalculations in fractions can lead to significant errors and potentially compromise structural integrity.
-
Sewing and Tailoring: Accurate measurements are crucial in sewing and tailoring to ensure a perfect fit.
-
Finance: Understanding fractions is essential for calculating interest, discounts, and proportions in financial transactions.
-
Data Analysis: Data analysis frequently involves working with fractions and percentages, requiring a thorough understanding of fractional arithmetic.
Tips for Mastering Fraction Addition
Here are some tips to help improve your skills in adding fractions and mixed numbers:
-
Practice Regularly: The more you practice, the more comfortable you'll become with the process.
-
Use Visual Aids: Visual aids, like diagrams or fraction circles, can help you visualize the fractions and understand the addition process.
-
Convert to Improper Fractions: While you can add mixed numbers directly, converting to improper fractions can simplify the process, particularly when dealing with more complex calculations.
-
Find a Common Denominator: When adding fractions with different denominators, remember to find a common denominator before adding the numerators.
-
Simplify Your Answer: Always simplify your answer to its lowest terms. For example, if your answer is 6/9, simplify it to ⅔.
Conclusion: The Importance of Fractional Accuracy
The seemingly simple question, "Do two 1⅓ cups equal 2⅔ cups?", reveals the importance of understanding fraction addition and the nuances of working with mixed numbers. Mistakes in these calculations can have significant consequences, from baking failures to errors in critical applications. By mastering these fundamental mathematical principles, you'll improve accuracy and efficiency in numerous aspects of your life. Regular practice and a clear understanding of the underlying concepts are key to success. Remember that precise measurements and calculations are essential for many activities, and this ability is a valuable skill to develop and hone. Through practice and attention to detail, you'll become more confident and adept at working with fractions.
Latest Posts
Latest Posts
-
Funeral Obituary Charlene Holt Cause Of Death
May 09, 2025
-
Which Hole Do You Stick It In
May 09, 2025
-
Lou Beatty Jr Related To Morgan Freeman
May 09, 2025
-
12 Letter Words With No Repeating Letters
May 09, 2025
-
How Much Is 40 Off Of 40
May 09, 2025
Related Post
Thank you for visiting our website which covers about Do Two 1 3 Cups Equal 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.