How Do I Find 2 3 Of A Number
Arias News
May 12, 2025 · 5 min read
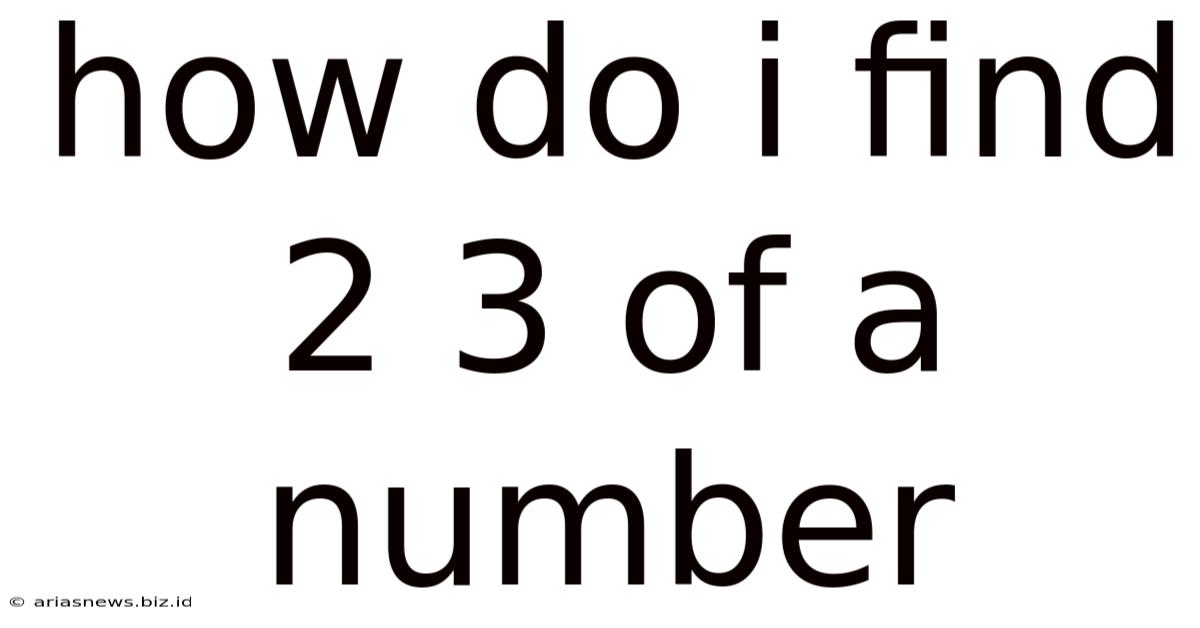
Table of Contents
How Do I Find ⅔ of a Number? A Comprehensive Guide
Finding a fraction of a number is a fundamental mathematical concept with widespread applications in everyday life, from calculating discounts and sales tax to understanding proportions in recipes and construction projects. This guide will walk you through various methods for finding two-thirds (⅔) of any number, explaining the underlying principles and offering practical examples to solidify your understanding. We'll explore different approaches, catering to various skill levels and preferences, ensuring you can confidently tackle this calculation in any context.
Understanding Fractions: A Quick Refresher
Before diving into the methods, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering.
In the fraction ⅔, 2 is the numerator and 3 is the denominator. This means we're interested in 2 out of 3 equal parts of a whole.
Method 1: Multiplication – The Direct Approach
The most straightforward way to find ⅔ of a number is to multiply the number by the fraction ⅔. This method directly applies the concept of fractions as a multiplicative operation.
Formula: (⅔) * Number = Result
Example: Let's find ⅔ of 18.
- Multiply the number by the numerator: 18 * 2 = 36
- Divide the result by the denominator: 36 / 3 = 12
Therefore, ⅔ of 18 is 12.
This method is efficient and easily adaptable to finding any fraction of a number. Simply replace ⅔ with the desired fraction and follow the same steps.
Practical Applications of Method 1
- Calculating discounts: If a product is 33% off (approximately ⅔), multiply the original price by ⅔ to find the discount amount.
- Recipe scaling: If a recipe calls for a certain amount of an ingredient, and you want to make ⅔ of the recipe, multiply each ingredient amount by ⅔.
- Determining proportions: In construction or design, finding ⅔ of a measurement might be necessary for accurate scaling and proportioning.
Method 2: Division Then Multiplication – A Step-by-Step Approach
This method breaks down the calculation into two simpler steps: first dividing by the denominator, then multiplying by the numerator. This can be particularly helpful for those who find fraction multiplication challenging.
Steps:
- Divide the number by the denominator (3): This finds the size of one-third (⅓) of the number.
- Multiply the result by the numerator (2): This combines two of these one-third portions to find two-thirds (⅔).
Example: Let's find ⅔ of 18 again using this method.
- Divide by the denominator: 18 / 3 = 6 (This is ⅓ of 18)
- Multiply by the numerator: 6 * 2 = 12
As you can see, we arrive at the same answer: 12.
Method 3: Decimal Conversion – Using Decimal Equivalents
Fractions can be converted to decimals for easier calculation, especially when using calculators. The decimal equivalent of ⅔ is approximately 0.6667 (the 6 repeats infinitely).
Steps:
- Convert the fraction to a decimal: ⅔ ≈ 0.6667
- Multiply the number by the decimal equivalent: Number * 0.6667 = Result
Example: Finding ⅔ of 18 using the decimal method.
- Decimal equivalent: ⅔ ≈ 0.6667
- Multiplication: 18 * 0.6667 ≈ 12.0006
Due to rounding, the answer might not be perfectly precise, but it's usually close enough for practical purposes.
Method 4: Simplifying the Fraction (Where Applicable)
Sometimes, the number you're working with might share a common factor with the denominator of the fraction. If so, simplifying the fraction before multiplication can make the calculation significantly easier.
Example: Let's find ⅔ of 24.
Notice that 24 is divisible by 3. We can simplify the problem by first dividing 24 by 3.
- Simplify: 24 / 3 = 8 (This is ⅓ of 24)
- Multiply: 8 * 2 = 16
Therefore, ⅔ of 24 is 16. This method avoids larger numbers and simplifies the calculation.
Choosing the Right Method: Practical Considerations
The best method depends on the numbers involved and your comfort level with different mathematical operations.
- Multiplication (Method 1): Most efficient for straightforward calculations, especially with larger numbers or when using a calculator.
- Division then Multiplication (Method 2): Helpful for those who prefer a step-by-step approach and find fraction multiplication challenging.
- Decimal Conversion (Method 3): Convenient when using a calculator and acceptable when minor rounding errors are insignificant.
- Simplification (Method 4): Most efficient when the number and the denominator share a common factor.
Advanced Applications and Problem Solving
The concept of finding ⅔ of a number extends to more complex scenarios:
- Finding ⅔ of a quantity with units: If you're dealing with units like meters, liters, or kilograms, remember to include the units in your answer. For example, ⅔ of 18 meters is 12 meters.
- Working with negative numbers: The same methods apply when dealing with negative numbers. Remember the rules of multiplication and division with negative numbers. For example, ⅔ of -18 is -12.
- Solving word problems: Many real-world problems involve finding a fraction of a quantity. Carefully read and interpret the problem to identify the relevant numbers and the fraction you need to use. For example, “A farmer harvested 27 apples, and sold ⅔ of them. How many apples did he sell?” (Answer: 18)
- Percentage Equivalents: Remember that ⅔ is approximately equal to 66.67%. Therefore, finding ⅔ of a number is the same as finding 66.67% of that number. This provides an alternative approach to solving these types of problems.
Mastering Fractions: Practice Makes Perfect
The key to mastering this skill is consistent practice. Try different examples with varying numbers, both positive and negative, and use different methods to build your confidence and understanding. The more you practice, the more naturally you'll be able to find ⅔ (or any fraction) of a number.
Conclusion: A Foundation for Future Math
Understanding how to find ⅔ of a number is a building block for many more advanced mathematical concepts. It lays the foundation for working with percentages, ratios, proportions, and ultimately, more complex algebraic equations. By mastering this seemingly simple skill, you're strengthening your mathematical foundation and enhancing your ability to solve a wide array of problems encountered in everyday life and more advanced studies. So, grab your calculator, or sharpen your pencil, and start practicing! You'll soon be a fraction-finding pro.
Latest Posts
Latest Posts
-
Difference Between 100 Meters And 100 Yards
May 12, 2025
-
What Is The Greatest Common Factor Of 60 And 90
May 12, 2025
-
Words Starting With J To Describe Someone
May 12, 2025
-
What Value Does The Represent In The Number
May 12, 2025
-
Which Equation Shows That 8 Is A Factor Of 32
May 12, 2025
Related Post
Thank you for visiting our website which covers about How Do I Find 2 3 Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.