How Many 1 8 In 1 2
Arias News
Mar 31, 2025 · 5 min read
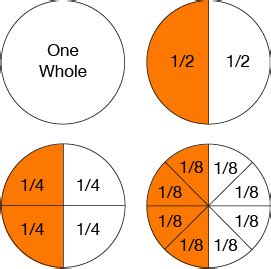
Table of Contents
How Many 1/8s are in 1/2? A Comprehensive Guide to Fraction Division
Understanding fractions is a cornerstone of mathematics, crucial for various applications from cooking and construction to advanced scientific calculations. A common question that often arises, particularly for students learning fractions, is "How many 1/8s are in 1/2?". This seemingly simple question opens the door to a deeper understanding of fraction division and its practical applications. This article will not only answer this question but will also delve into the underlying principles, providing you with the tools to tackle similar fraction problems with confidence.
Understanding Fractions: A Quick Refresher
Before we dive into the specific problem, let's briefly review the fundamentals of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) indicates the whole is divided into two equal parts. Similarly, 1/8 represents one part out of a whole divided into eight equal parts.
Different Approaches to Solving "How Many 1/8s are in 1/2?"
There are several ways to solve the problem of determining how many 1/8s are in 1/2. Let's explore the most common methods:
Method 1: Visual Representation
Imagine a pizza cut into eight equal slices. Each slice represents 1/8 of the pizza. Now, imagine taking half (1/2) of the pizza. How many of the 1/8 slices do you have? You'd have four slices, which is equivalent to 4/8. Therefore, there are four 1/8s in 1/2.
This visual approach is particularly helpful for beginners as it provides a concrete understanding of the concept. Using visual aids like diagrams or real-world objects can greatly aid comprehension.
Method 2: Fraction Division
This method involves dividing the fraction 1/2 by the fraction 1/8. To divide fractions, we follow these steps:
-
Invert (reciprocate) the second fraction: The reciprocal of 1/8 is 8/1 (or simply 8).
-
Multiply the first fraction by the reciprocal of the second fraction: (1/2) * (8/1) = 8/2
-
Simplify the resulting fraction: 8/2 simplifies to 4.
Therefore, there are four 1/8s in 1/2. This method offers a more formal mathematical approach, applicable to a wider range of fraction problems.
Method 3: Finding a Common Denominator
This method involves converting both fractions to have the same denominator. Since the denominator of 1/8 is 8, let's convert 1/2 to have a denominator of 8:
-
Find the equivalent fraction of 1/2 with a denominator of 8: To get from 2 to 8, we multiply by 4. Therefore, we must multiply both the numerator and denominator of 1/2 by 4: (1 * 4) / (2 * 4) = 4/8
-
Compare the numerators: Now we have 4/8 and 1/8. The numerator of 4/8 (which is 4) indicates that there are four 1/8s in 4/8 (which is equivalent to 1/2).
This method emphasizes the equivalence of fractions and the importance of finding a common denominator when comparing or operating on fractions.
Expanding on Fraction Division: More Complex Examples
Now that we've solved the problem of how many 1/8s are in 1/2, let's explore more complex examples to solidify your understanding of fraction division:
Example 1: How many 1/4s are in 2/3?
- Invert the second fraction: 4/1
- Multiply: (2/3) * (4/1) = 8/3
- Simplify: 8/3 = 2 and 2/3
Therefore, there are 2 and 2/3 1/4s in 2/3.
Example 2: How many 3/5s are in 2?
- Express 2 as a fraction: 2/1
- Invert the second fraction: 5/3
- Multiply: (2/1) * (5/3) = 10/3
- Simplify: 10/3 = 3 and 1/3
Therefore, there are 3 and 1/3 3/5s in 2.
These examples highlight the versatility of the fraction division method. Remember, the key is to invert the second fraction and then multiply.
Practical Applications of Fraction Division
Understanding fraction division is not merely an academic exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often require fractional measurements. Knowing how to divide fractions is crucial for scaling recipes up or down. For example, if a recipe calls for 1/2 cup of flour, but you only want to make half the recipe, you need to determine how much flour (1/4 cup) you need.
-
Construction and Carpentry: Precise measurements are essential in construction. Dividing fractions helps in accurately cutting materials to the required sizes.
-
Sewing and Tailoring: Creating garments involves precise measurements and fabric cutting. Understanding fractions is vital for accurate pattern making and fabric utilization.
-
Finance and Budgeting: Managing finances often involves working with fractions of amounts. Dividing fractions helps in calculating percentages and proportions for budgeting and investments.
-
Science and Engineering: Many scientific and engineering calculations involve fractions. Understanding fraction division is critical for accurate data analysis and problem-solving.
Tips and Tricks for Mastering Fraction Division
-
Practice regularly: The key to mastering any mathematical concept is consistent practice. Work through various examples, starting with simpler problems and gradually increasing the complexity.
-
Use visual aids: Diagrams and real-world objects can help visualize fraction division, making it easier to grasp the concept.
-
Break down complex problems: If you encounter a complex problem, break it down into smaller, manageable steps.
-
Check your answers: Always check your answers to ensure accuracy. You can do this by reversing the operation or using a different method to solve the problem.
Conclusion: Beyond the Basics of Fraction Division
This article has comprehensively explored the question, "How many 1/8s are in 1/2?", providing multiple methods for solving the problem and expanding upon the broader concept of fraction division. By understanding the underlying principles and practicing regularly, you can confidently tackle various fraction problems in various contexts. Remember, mastering fractions is a valuable skill with wide-ranging applications in everyday life and various fields of study. So, keep practicing, and you'll soon be a fraction division expert!
Latest Posts
Latest Posts
-
What Is The Answer For A Subtraction Problem Called
Apr 01, 2025
-
How Do You Say Say Cheese In Spanish
Apr 01, 2025
-
How Tall Is 33 Inches In Feet
Apr 01, 2025
-
How Many Zeros Are In 1 5 Million
Apr 01, 2025
-
How Do You Say Caleb In Spanish
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many 1 8 In 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
