How Many 3 8 Are In 1
Arias News
May 08, 2025 · 5 min read
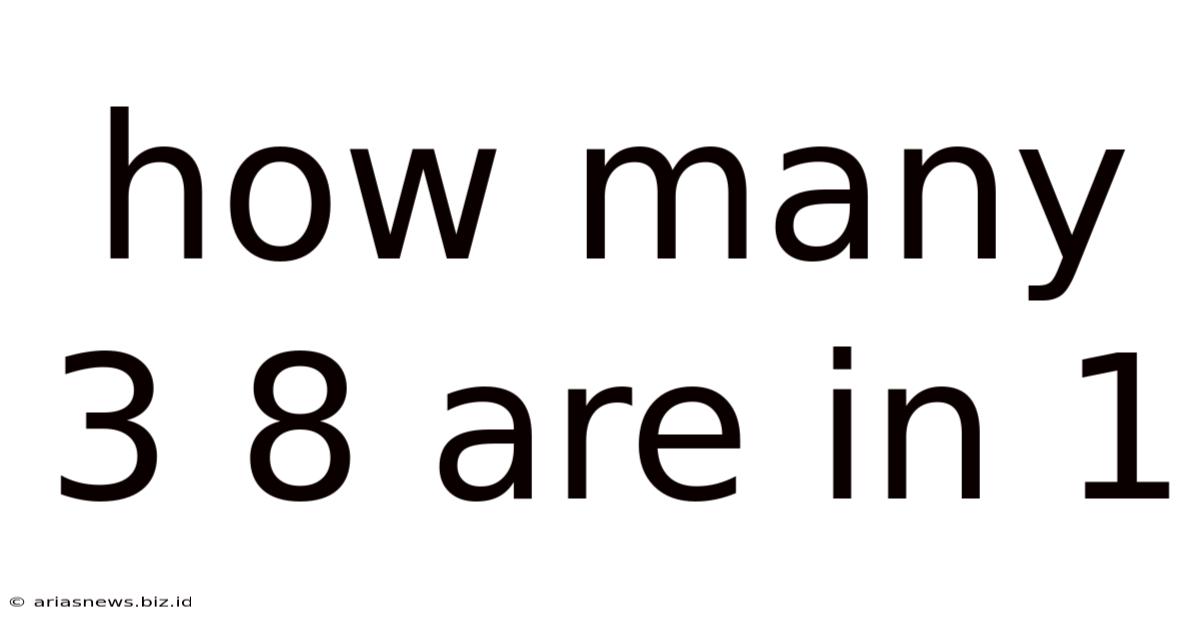
Table of Contents
How Many 3/8s Are in 1? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 3/8s are in 1?", opens a door to a fascinating exploration of fractions, division, and their practical applications. While the answer might seem immediately obvious to some, understanding the underlying principles is crucial for mastering more complex mathematical concepts. This article will not only answer the question directly but also delve into the "why" behind the solution, providing a comprehensive understanding of the processes involved.
Understanding Fractions: Building Blocks of Mathematics
Before diving into the specifics of our problem, let's establish a firm understanding of fractions. A fraction represents a part of a whole. It's composed of two key elements:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our case, 3/8 signifies that we have 3 parts out of a total of 8 equal parts. Visualizing this using a pie chart or a bar divided into eight sections can be incredibly helpful.
The Question: How Many 3/8s Are in 1?
The question, "How many 3/8s are in 1?", essentially asks how many times 3/8 fits into the whole number 1. This is a division problem in disguise. To solve it, we need to perform the division:
1 ÷ (3/8)
Solving the Division: Two Approaches
There are two primary methods to solve this division problem:
Method 1: The Reciprocal Method
This method utilizes the concept of reciprocals. The reciprocal of a fraction is obtained by swapping its numerator and denominator. The reciprocal of 3/8 is 8/3. To divide by a fraction, we multiply by its reciprocal:
1 ÷ (3/8) = 1 × (8/3) = 8/3
This result, 8/3, is an improper fraction (where the numerator is larger than the denominator). To express it as a mixed number (a whole number and a fraction), we perform the division:
8 ÷ 3 = 2 with a remainder of 2.
Therefore, 8/3 is equal to 2 and 2/3.
So, there are 2 and 2/3 of 3/8s in 1.
Method 2: The Common Denominator Method
This approach involves converting both numbers into fractions with a common denominator. Since 1 can be represented as 8/8, we can now perform the division:
(8/8) ÷ (3/8)
When dividing fractions with a common denominator, we simply divide the numerators:
8 ÷ 3 = 8/3
This again gives us the improper fraction 8/3, which, as shown above, simplifies to 2 and 2/3.
Practical Applications and Real-World Examples
Understanding this type of fractional division is essential in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. If a recipe calls for 3/8 cup of flour per serving and you want to make a batch yielding one cup of servings, this calculation determines the number of servings you'll get.
-
Construction and Measurement: Precision in construction and engineering frequently involves fractions. Calculating how many 3/8-inch pieces can be cut from a 1-inch long rod is a direct application of this problem.
-
Data Analysis and Statistics: Working with datasets often involves understanding proportions and ratios, which inherently use fractions. Calculating percentages or analyzing samples involves similar fractional divisions.
-
Financial Calculations: Dividing a whole amount (like a budget) into smaller fractional parts is commonplace in financial planning. Allocating a budget based on fractional percentages or requirements exemplifies the practical relevance.
Extending the Concept: Solving Similar Problems
The principles discussed here can be applied to a broader range of problems involving fractional division. For example, let's consider the following:
-
How many 2/5s are in 1? Following the same methods, we would have 1 ÷ (2/5) = 1 × (5/2) = 5/2 = 2 and 1/2.
-
How many 5/12s are in 2? Here, we'd solve 2 ÷ (5/12) = 2 × (12/5) = 24/5 = 4 and 4/5.
The key is always to remember the reciprocal method or the common denominator method for solving the division.
Beyond the Basics: Deeper Exploration of Fractions
This article provides a foundational understanding of fractional division. For those seeking to delve deeper, exploring the following concepts would be beneficial:
-
Complex Fractions: These involve fractions within fractions, adding another layer of complexity to the division process.
-
Mixed Numbers and Improper Fractions: Mastering the conversion between these formats is critical for efficient problem-solving.
-
Least Common Multiple (LCM) and Greatest Common Factor (GCF): These concepts are essential for simplifying fractions and finding common denominators.
-
Decimal Representation of Fractions: Understanding how to convert fractions to decimals and vice-versa enhances problem-solving flexibility.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question of "How many 3/8s are in 1?" has led us on a journey through the fundamentals of fractions and division. By understanding the principles involved, we equip ourselves not only to solve this specific problem but also to tackle a wide range of similar mathematical challenges encountered in everyday life, academic pursuits, and professional settings. The ability to work confidently with fractions is a valuable skill that opens doors to more advanced mathematical concepts and real-world applications. So, embrace the power of fractions, and let your understanding grow!
Latest Posts
Latest Posts
-
What Is A Group Of Women Called
May 08, 2025
-
How Long Can You Swim After Belly Piercing
May 08, 2025
-
How Many Potato Chips In A Bag
May 08, 2025
-
7 How Many Nickels Are There In Seventeen Dollars
May 08, 2025
-
What Is The Last Name Of Romeo And Juliet
May 08, 2025
Related Post
Thank you for visiting our website which covers about How Many 3 8 Are In 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.