How Many Right Angles Does A Square Have
Arias News
Apr 01, 2025 · 6 min read
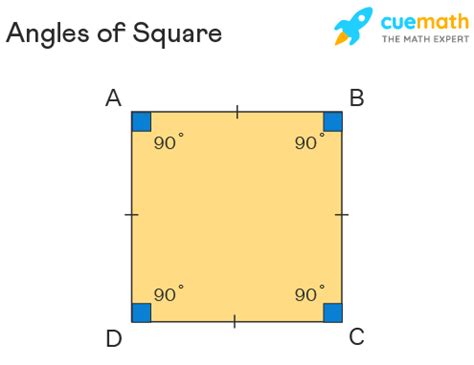
Table of Contents
How Many Right Angles Does a Square Have? A Deep Dive into Geometry
The seemingly simple question, "How many right angles does a square have?" opens a door to a fascinating exploration of geometry, its fundamental concepts, and its applications in various fields. While the immediate answer is straightforward, delving deeper reveals the rich mathematical underpinnings that define squares and their properties. This article will not only answer the question definitively but will also explore the related concepts of angles, shapes, and the significance of right angles in mathematics and beyond.
Understanding Angles: The Foundation of Geometry
Before tackling the central question, let's establish a solid understanding of angles. An angle is formed by two rays, or line segments, that share a common endpoint called the vertex. Angles are measured in degrees, with a right angle measuring exactly 90 degrees. This is often represented visually by a small square drawn in the corner of the angle. Other types of angles include:
- Acute angles: Angles measuring less than 90 degrees.
- Obtuse angles: Angles measuring more than 90 degrees but less than 180 degrees.
- Straight angles: Angles measuring exactly 180 degrees, forming a straight line.
- Reflex angles: Angles measuring more than 180 degrees but less than 360 degrees.
Understanding these different types of angles is crucial for comprehending the properties of various geometric shapes, including our focus today: the square.
Defining a Square: Properties and Characteristics
A square is a two-dimensional geometric shape defined by its distinct characteristics:
- Four sides: A square possesses four straight sides of equal length. This equality of sides is a defining characteristic, differentiating it from other quadrilaterals.
- Four right angles: This is the key property relevant to our central question. Each of the four corners of a square forms a perfect 90-degree angle, a right angle.
- Parallel sides: Opposite sides of a square are parallel to each other. This parallelism contributes to the square's stability and symmetry.
- Equal diagonals: The diagonals of a square (lines connecting opposite corners) are equal in length and bisect each other at a right angle.
These properties are interconnected and define the unique nature of a square. The presence of four right angles is fundamental to its classification as a square, and it distinguishes it from other quadrilaterals like rectangles, rhombuses, and parallelograms.
The Answer: A Square Has Four Right Angles
Therefore, to finally answer the question: a square has four right angles. This is an inherent property of a square, a defining characteristic that distinguishes it from other shapes. The presence of these four 90-degree angles contributes to the square's symmetry, stability, and its wide-ranging applications in various fields.
The Significance of Right Angles in Geometry and Beyond
Right angles are not just a characteristic of squares; they are fundamental to many aspects of geometry and mathematics. They are used in:
- Coordinate systems: Right angles form the basis of Cartesian coordinate systems, enabling the precise location of points in two or three dimensions.
- Trigonometry: Right-angled triangles are central to trigonometry, enabling the calculation of angles and sides of triangles.
- Construction and engineering: Right angles are crucial in construction and engineering for creating stable and accurate structures. Buildings, bridges, and other structures rely heavily on right angles for their structural integrity.
- Computer graphics and design: Right angles are fundamental in computer graphics and design for creating precise and accurate representations of objects and scenes.
- Art and design: The visual appeal of many artistic and design elements stems from the use of right angles and the symmetry they create.
The significance of right angles extends beyond the realm of pure mathematics into numerous practical applications in the real world.
Exploring Related Shapes: Rectangles, Rhombuses, and More
While squares are unique, understanding their relationship to other quadrilaterals provides further insight into geometrical concepts:
- Rectangles: Rectangles share the property of four right angles with squares but have sides that are not necessarily of equal length. A square can be considered a special type of rectangle where all sides are equal.
- Rhombuses: Rhombuses have four equal sides, but their angles are not necessarily right angles. A square is a special type of rhombus where all angles are right angles.
- Parallelograms: Parallelograms have opposite sides that are parallel, but their angles and side lengths may vary. Both rectangles and rhombuses are types of parallelograms.
Understanding the relationships between these shapes helps to build a comprehensive understanding of geometric concepts and their properties.
Practical Applications of Squares and Right Angles
The properties of squares and the significance of right angles are evident in numerous real-world applications:
- Architecture and construction: Buildings, bridges, and other structures utilize the stability and symmetry offered by square and rectangular shapes, reinforced by the use of right angles in their construction.
- Engineering: Mechanical designs, circuit boards, and other engineering applications often employ square and rectangular shapes because of their ease of construction and predictable properties.
- Games and puzzles: Squares are commonly used in various games and puzzles, providing a structured and visually appealing playing field. Examples include chessboards, Sudoku grids, and crossword puzzles.
- Art and design: The symmetry and stability of squares and right angles are utilized in various art forms and design principles to create visually appealing and balanced compositions.
The prevalence of squares and right angles in daily life highlights their importance and practical significance.
Beyond the Basics: Advanced Concepts Related to Squares
For those seeking a deeper understanding, exploring advanced concepts related to squares can further enhance geometric knowledge:
- Area and perimeter: Calculating the area and perimeter of squares involves simple formulas that rely on the lengths of their sides.
- Rotation and symmetry: Squares exhibit rotational symmetry, meaning they can be rotated by 90, 180, or 270 degrees and still look the same. They also possess reflectional symmetry.
- Tessellations: Squares are particularly well-suited for creating tessellations, which are patterns formed by repeatedly tiling a shape to cover a plane without gaps or overlaps.
- Higher dimensions: The concept of a square can be extended to higher dimensions, leading to the exploration of cubes (three dimensions) and hypercubes (four or more dimensions).
These more advanced concepts demonstrate the richness and complexity of geometric principles related to squares and right angles.
Conclusion: The Enduring Importance of Squares and Right Angles
The seemingly simple question, "How many right angles does a square have?" has led us on a journey through the fundamental concepts of geometry, exploring the properties of squares, the significance of right angles, and their widespread applications. While the answer – four – is straightforward, the underlying principles are profound and far-reaching, shaping our understanding of the world around us and fueling countless innovations in mathematics, engineering, and art. The enduring importance of squares and right angles underscores their fundamental role in our understanding and shaping of the world.
Latest Posts
Latest Posts
-
Items That Start With The Letter K
Apr 02, 2025
-
Side Circle Does A 3 Inch By 3 Inch Square Represent
Apr 02, 2025
-
How Much Is One Fourth Pound Of Butter
Apr 02, 2025
-
What Is The Greatest Common Factor Of 7 And 14
Apr 02, 2025
-
Which Is The Best Definition Of Value
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How Many Right Angles Does A Square Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
