How Many Sig Figs Are In 10.0
Arias News
May 08, 2025 · 5 min read
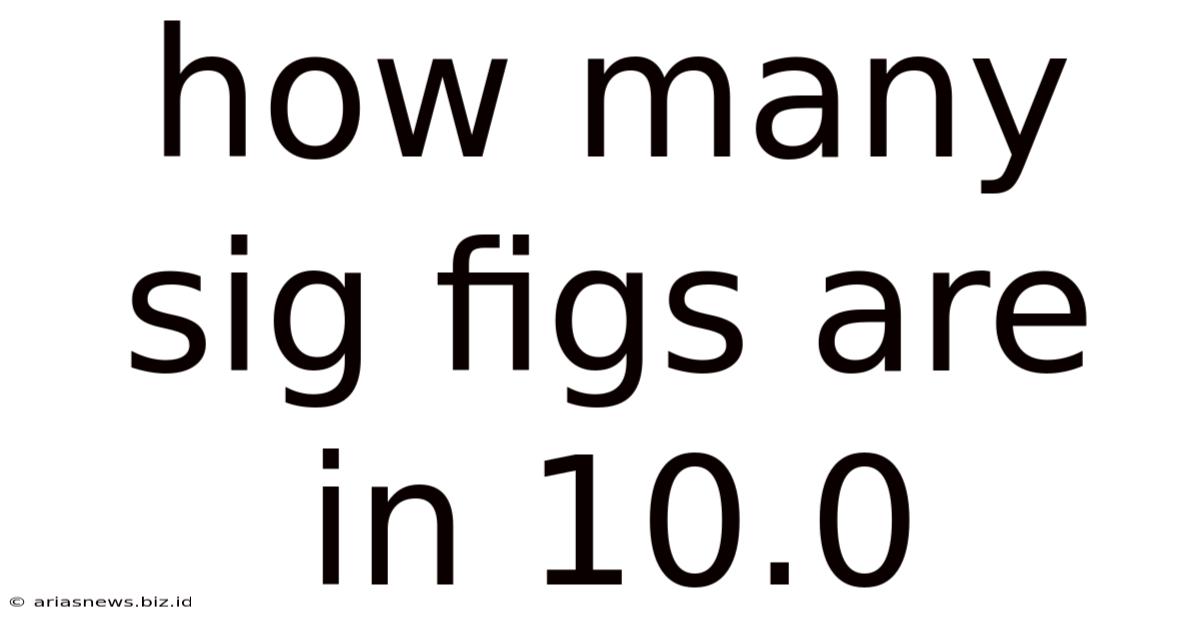
Table of Contents
How Many Significant Figures Are in 10.0? A Deep Dive into Significant Figures
Determining the number of significant figures (sig figs) in a number might seem straightforward, but nuances exist, especially when dealing with numbers like 10.0. This comprehensive guide will delve into the intricacies of significant figures, focusing specifically on the number 10.0, and provide you with a robust understanding of this essential concept in scientific notation and measurement.
Understanding Significant Figures
Significant figures are the digits in a number that carry meaning contributing to its precision. They represent the level of accuracy of a measurement or calculation. Understanding sig figs is crucial in scientific fields, engineering, and any discipline requiring precise numerical representation. The rules governing significant figures ensure consistent communication of measurement uncertainty.
Rules for Determining Significant Figures
Several rules guide the determination of significant figures:
- Non-zero digits are always significant. For example, in the number 234, all three digits are significant.
- Zeros between non-zero digits are significant. In 2004, the zero is significant.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant. They merely serve to locate the decimal point. For example, in 0.0025, only 2 and 5 are significant.
- Trailing zeros (zeros to the right of the last non-zero digit) are significant only if the number contains a decimal point. This is where the confusion often arises. In 100, only one sig fig is present. However, in 100. or 100.0, all digits are significant. This crucial distinction highlights the importance of decimal points in indicating precision.
- Trailing zeros in a number without a decimal point are ambiguous and should be avoided. Scientific notation is preferred to eliminate ambiguity.
The Case of 10.0: Three Significant Figures
Now, let's address the central question: how many significant figures are in 10.0?
The answer is three.
Applying the rules above:
- The digit 1 is non-zero and therefore significant.
- The zero between the 1 and the final zero is significant.
- The trailing zero after the decimal point is significant because the decimal point is present.
The inclusion of the decimal point and the trailing zero explicitly indicates a higher level of precision than simply writing 10. 10 could represent any value between 9.5 and 10.5, while 10.0 implies a value between 9.95 and 10.05. The additional zero signifies a measurement made to a higher degree of accuracy.
Significant Figures and Scientific Notation
Scientific notation provides a clear and unambiguous way to express numbers and their significant figures, especially for very large or very small numbers. It involves representing a number as a coefficient multiplied by a power of 10. The coefficient always has only one non-zero digit before the decimal point.
For example, 10.0 can be written in scientific notation as 1.00 x 10¹. In this representation, the three significant figures are clearly visible in the coefficient. This method removes any ambiguity associated with trailing zeros.
Practical Implications of Significant Figures
Understanding significant figures is paramount in many fields:
- Chemistry: Accurate stoichiometric calculations and chemical analyses require precise handling of significant figures. Incorrect handling can lead to significant errors in experimental results and conclusions.
- Physics: Accurate representation of measurements and calculation of physical quantities such as velocity, acceleration, and force depend heavily on correctly accounting for significant figures.
- Engineering: Engineering designs and calculations must be precise. Errors due to incorrect handling of significant figures can have severe consequences, including structural failures and equipment malfunctions.
- Data Analysis: Accurate interpretation of data and statistical analysis rely on understanding the precision and accuracy represented by significant figures.
Avoiding Common Mistakes with Significant Figures
Several common mistakes occur when working with significant figures:
- Ignoring trailing zeros: Failing to recognize the significance of trailing zeros after a decimal point is a frequent error.
- Misinterpreting leading zeros: Leading zeros before the first non-zero digit are not significant and should not be counted.
- Inconsistent rounding: Inconsistent application of rounding rules can lead to accumulation of errors, especially in multi-step calculations. Rounding should be done at the final step of a calculation to minimize error propagation.
- Incorrect application of mathematical operations: Operations involving significant figures require attention to the rules for addition, subtraction, multiplication, and division, with the final answer reflecting the least precise measurement.
Advanced Concepts: Significant Figures in Calculations
When performing calculations with numbers containing significant figures, specific rules apply:
- Addition and Subtraction: The result should have the same number of decimal places as the measurement with the fewest decimal places.
- Multiplication and Division: The result should have the same number of significant figures as the measurement with the fewest significant figures.
For example:
10.0 + 1.23 = 11.2 (limited to one decimal place)
10.0 x 1.23 = 12 (limited to two significant figures)
These rules ensure that the final result doesn't imply a level of precision greater than what is justified by the input measurements.
Conclusion: The Importance of Precision
The number 10.0 clearly illustrates the importance of paying close attention to detail when dealing with significant figures. The seemingly small addition of a decimal point and a trailing zero drastically alters the level of precision conveyed. Mastering the rules and nuances of significant figures is essential for anyone working with numerical data, ensuring accuracy, reliability, and clear communication of results across various scientific and engineering disciplines. Understanding and correctly applying these rules guarantees precision and reduces errors, ultimately contributing to the reliability and validity of scientific and engineering endeavors. Remember, precision is paramount – and in the realm of numbers, it all begins with the correct identification of significant figures.
Latest Posts
Latest Posts
-
Where Can I Watch Kiss X Sis
May 08, 2025
-
Which Shape Is A Parallelogram But Not A Rhombus
May 08, 2025
-
Is Edie Falco In Orange Is The New Black
May 08, 2025
-
What Are Quad Seats In An Suv
May 08, 2025
-
Was Jackie Cooper In The Wizard Of Oz
May 08, 2025
Related Post
Thank you for visiting our website which covers about How Many Sig Figs Are In 10.0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.