How Many Times Can 8 Go Into 60
Arias News
Apr 02, 2025 · 5 min read
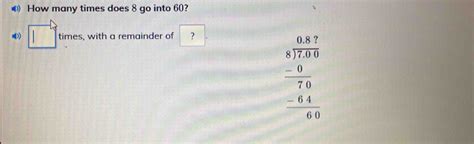
Table of Contents
How Many Times Can 8 Go Into 60? A Deep Dive into Division
The seemingly simple question, "How many times can 8 go into 60?" opens the door to a fascinating exploration of division, remainders, and their practical applications in various fields. While a quick calculation might suffice for some, understanding the underlying principles offers a more profound appreciation of mathematical concepts and problem-solving strategies. This comprehensive guide will not only answer the initial question but also delve into related concepts, showcasing the multifaceted nature of this seemingly basic arithmetic operation.
The Straightforward Answer
The most direct answer to the question, "How many times can 8 go into 60?" is 7, with a remainder of 4. This is because 8 multiplied by 7 equals 56, and 60 minus 56 equals 4. This simple division problem forms the bedrock of more complex mathematical operations.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. In the context of "How many times can 8 go into 60?", we're essentially asking how many times the number 8 can be subtracted from 60 before the remaining value is less than 8. The result of this division is called the quotient, which in this case is 7. The amount left over after the division is the remainder, which is 4.
The Importance of Remainders: Remainders aren't simply leftovers; they are crucial pieces of information. They highlight that the initial quantity (60) isn't perfectly divisible by the divisor (8). In real-world applications, understanding the remainder can be critical. For example, if you have 60 apples and want to divide them equally among 8 friends, each friend gets 7 apples, and you have 4 apples remaining.
Different Ways to Represent Division
The division problem "How many times can 8 go into 60?" can be represented in several ways:
-
Long Division: This traditional method involves systematically subtracting multiples of the divisor from the dividend until the remainder is less than the divisor.
-
Short Division: A quicker method for smaller numbers, often used mentally.
-
Fractions: The division can also be expressed as a fraction: 60/8. This fraction can be simplified to 15/2 or expressed as a mixed number 7 1/2.
-
Decimal Representation: The division can be represented as a decimal by continuing the division process beyond the remainder, resulting in 7.5.
Real-World Applications: Beyond the Classroom
Understanding division and remainders extends far beyond the confines of a mathematics classroom. Here are some practical applications:
1. Resource Allocation:
-
Fair Sharing: As illustrated with the apple example, dividing resources equally among a group often leaves a remainder. Understanding how to handle the remainder is crucial for equitable distribution.
-
Inventory Management: Businesses use division to track inventory levels and determine when to reorder supplies. Remainders can indicate the need for additional stock to meet future demand.
-
Project Planning: Dividing a large project into smaller tasks often results in unequal task sizes. The remainder represents the extra work needed to complete the project.
2. Measurement and Conversions:
-
Unit Conversions: Converting between units of measurement, such as meters to feet or liters to gallons, frequently involves division and results in remainders. These remainders must be correctly accounted for in the final converted value.
-
Geometry and Area Calculation: Determining the number of tiles needed to cover a floor or the number of pieces of wood to build a fence often requires division, with the remainder representing extra material or waste.
3. Programming and Computer Science:
-
Looping and Iteration: Programming relies heavily on division and remainders. For instance, determining if a number is even or odd involves checking for a remainder of 0 when divided by 2.
-
Data Structures and Algorithms: Many algorithms use division and remainders for efficient data manipulation and processing. Hash tables, for example, often use the modulo operator (which gives the remainder) to distribute data.
-
Cryptography: Modulo arithmetic, which centers around remainders, plays a fundamental role in modern cryptography algorithms.
4. Everyday Life:
-
Sharing Costs: When splitting a restaurant bill among friends, the remainder represents any extra change that needs to be accounted for.
-
Cooking and Baking: Recipes often require dividing ingredients into specific portions. Remainders might suggest adjusting the recipe to avoid waste.
Exploring Related Mathematical Concepts
Understanding the division problem "How many times can 8 go into 60?" also provides a foundation for exploring more advanced mathematical concepts:
-
Modular Arithmetic: This branch of number theory focuses on remainders and their properties. The modulo operator (%) is a crucial part of modular arithmetic, frequently used in computer science and cryptography.
-
Prime Numbers: Prime numbers are integers greater than 1 that are only divisible by 1 and themselves. Understanding division and prime factorization is critical in various areas of mathematics.
-
Factors and Multiples: Identifying factors and multiples of a number helps to simplify division and understand the relationships between different numbers.
Conclusion: The Power of a Simple Division Problem
The seemingly simple question, "How many times can 8 go into 60?", unravels into a rich exploration of division, remainders, and their pervasive applications in various fields. While the answer – 7 with a remainder of 4 – is straightforward, the underlying principles and practical implications extend far beyond this basic calculation. By understanding the nuances of division, we gain a deeper appreciation for the power of mathematics in solving everyday problems and driving innovation across diverse disciplines. This comprehensive examination highlights the importance of not just finding the answer, but also understanding the 'why' behind it, leading to a more robust and applicable understanding of mathematical concepts.
Latest Posts
Latest Posts
-
Things That Look Like The Letter A
Apr 03, 2025
-
How Long Can Your Hair Grow In A Lifetime
Apr 03, 2025
-
How Many Teaspoons In A Pound Of Salt
Apr 03, 2025
-
One And One Tenth As A Decimal
Apr 03, 2025
-
How Many Grams Are In One Liter Of Water
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Many Times Can 8 Go Into 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
