If A Right Circular Cone Is Intersected By A Plane
Arias News
Mar 26, 2025 · 6 min read
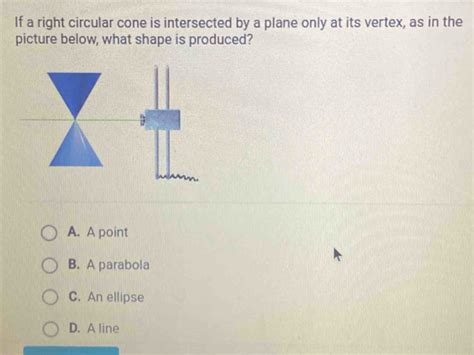
Table of Contents
If a Right Circular Cone is Intersected by a Plane: A Comprehensive Exploration
The intersection of a right circular cone with a plane is a fundamental concept in geometry with far-reaching applications in various fields, from engineering and architecture to computer graphics and art. Understanding the different types of curves that can result from this intersection is crucial for solving problems related to three-dimensional shapes and spatial reasoning. This article delves deep into this fascinating topic, exploring the various possibilities and the geometric properties of the resulting curves.
Understanding the Basics: The Right Circular Cone
Before exploring the intersections, let's define our primary shape: the right circular cone. A right circular cone is a three-dimensional geometric solid that is formed by connecting a circular base to a single point called the apex or vertex. The line segment connecting the apex to the center of the base is called the axis of the cone. The slant height is the distance from the apex to any point on the circumference of the base. Crucially, in a right circular cone, the axis is perpendicular to the base.
The Plane's Role: Angle and Position
The nature of the intersection curve depends critically on the angle at which the plane intersects the cone and its position relative to the cone's axis and base. Different angles and positions lead to remarkably different results. Let's analyze these factors:
The Angle of Intersection
Imagine a plane slicing through the cone. The angle this plane makes with the axis of the cone determines the type of curve generated. This angle is crucial in classifying the intersections.
The Position of the Plane
The plane's position relative to the cone's axis and base further influences the intersection. Is the plane parallel to the base? Does it intersect the base? Does it pass through the apex? These factors significantly alter the shape of the resulting curve.
Types of Conic Sections: The Intersections
The intersection of a plane and a right circular cone can result in several distinct types of curves, collectively known as conic sections. These include:
1. Circle: A Parallel Plane
If the plane is parallel to the base of the cone and intersects the cone above the apex, the resulting intersection is a circle. The circle's size depends on the distance of the plane from the apex. The closer the plane is to the apex, the smaller the circle; the farther away, the larger the circle.
Key Characteristics: All points on the circle are equidistant from a central point.
2. Ellipse: An Oblique Plane
When the plane intersects the cone at an angle, such that it intersects all generators (lines from the apex to the base), but does not pass through the apex, the result is an ellipse. An ellipse is a closed curve where the sum of the distances from any point on the curve to two fixed points (called foci) is constant.
Key Characteristics: Two foci, a major axis (longest diameter), and a minor axis (shortest diameter). The shape of the ellipse changes depending on the angle of the intersecting plane.
3. Parabola: A Parallel Plane through One Generator
A parabola is formed when the intersecting plane is parallel to exactly one generator of the cone. This means the plane intersects only one half of the double cone.
Key Characteristics: A single focus and a directrix (a line). Every point on the parabola is equidistant from the focus and the directrix.
4. Hyperbola: A Plane Intersecting Both Halves of the Double Cone
If the plane intersects both halves of the double cone (imagine extending the cone infinitely in both directions), the resulting intersection is a hyperbola. A hyperbola consists of two separate, mirror-image curves.
Key Characteristics: Two foci, two branches, and two asymptotes (lines that the branches approach but never touch).
Degenerate Cases: Special Intersections
There are also instances where the intersection results in a degenerate conic section. These occur under specific circumstances:
1. A Point: Plane Passing Through the Apex
If the plane passes through the apex of the cone and only touches the apex, the intersection is a single point. This is a degenerate case of all conic sections.
2. A Line: Plane Containing the Axis
If the plane contains the axis of the cone, the intersection will be a line segment. This is another degenerate case.
3. Two Intersecting Lines: Plane Through the Apex Intersecting the Cone
If a plane passes through the apex of the cone and intersects the cone's surface at more than a single point, the intersection forms two intersecting lines. This case falls under the degenerate classification.
Applications and Significance
The study of conic sections and the intersection of a plane with a cone has numerous practical applications across diverse fields:
-
Astronomy: Kepler's laws of planetary motion describe planetary orbits as ellipses, a direct consequence of gravitational forces and the concept of conic sections.
-
Engineering and Architecture: Parabolic shapes are used in designing bridges, reflectors, and satellite dishes due to their unique reflective properties. Elliptical shapes are often used in architecture and engineering for their aesthetic appeal and structural integrity.
-
Computer Graphics: Conic sections are fundamental in computer graphics for creating realistic and smooth curves in 2D and 3D modeling and animation.
-
Optics: The properties of ellipses, parabolas, and hyperbolas are vital in understanding reflection and refraction of light in lenses and mirrors.
-
Mathematics: Conic sections serve as fundamental examples in various areas of mathematics, including calculus, analytic geometry, and linear algebra.
Advanced Concepts: Beyond the Basics
The intersection of a cone and a plane opens doors to advanced geometric concepts. Exploring these can significantly enrich understanding:
-
Equation of Conic Sections: Each conic section can be represented by a unique equation in Cartesian coordinates. Deriving and understanding these equations enhances our ability to manipulate and analyze these curves algebraically.
-
Focal Properties: The foci of ellipses, parabolas, and hyperbolas play a crucial role in their reflective and refractive properties, leading to diverse applications in optics and engineering.
-
Eccentricity: The eccentricity of a conic section is a dimensionless quantity that describes the shape of the curve. It's a powerful tool for characterizing and classifying conic sections.
-
Polar Coordinates: Representing conic sections in polar coordinates simplifies calculations and provides alternative perspectives on their geometric properties.
Conclusion: A Rich and Versatile Geometric Concept
The intersection of a right circular cone with a plane is a remarkably rich and multifaceted topic. Understanding the various conic sections – circles, ellipses, parabolas, and hyperbolas – and their degenerate forms provides a robust foundation for tackling more complex geometric problems. The wide-ranging applications of these curves underscore their significance in science, engineering, and art, making the study of conic sections a worthwhile endeavor for students and professionals alike. Further exploration into the advanced concepts mentioned above will only enhance one's understanding and ability to apply this powerful geometric concept.
Latest Posts
Latest Posts
-
How Do You Say Karen In Spanish
Mar 29, 2025
-
Chandra Currelley Heaven Waits For Me Lyrics
Mar 29, 2025
-
How Many Cups Are In 1 Pound Of Peanut Butter
Mar 29, 2025
-
721 Lbs Per Week Into Kg Per Second
Mar 29, 2025
-
How Many Cups In A Pound Of Cooked Ground Beef
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about If A Right Circular Cone Is Intersected By A Plane . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
