Is 1 2 Greater Than 1 8
Arias News
May 10, 2025 · 5 min read
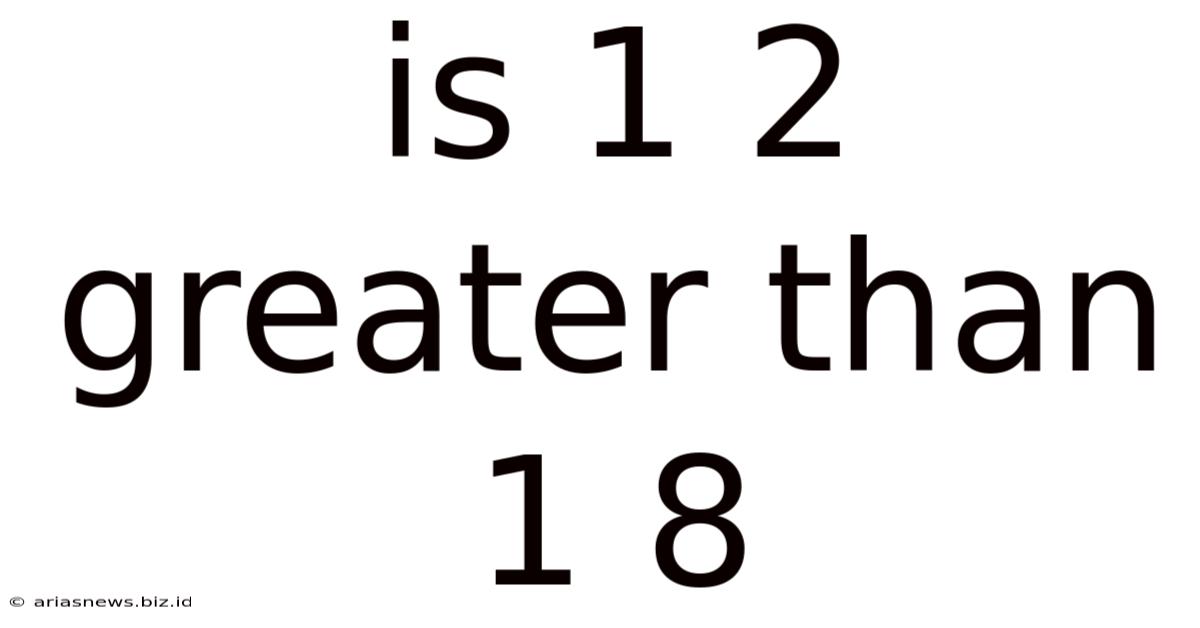
Table of Contents
Is 1/2 Greater Than 1/8? A Deep Dive into Fraction Comparison
The question, "Is 1/2 greater than 1/8?" might seem trivial at first glance. For many, the answer is immediately apparent. However, a deeper exploration of this seemingly simple comparison offers a valuable opportunity to solidify our understanding of fractions, explore various comparison methods, and delve into the broader context of numerical reasoning. This article will not only answer the question definitively but will also equip you with the tools and knowledge to confidently compare any two fractions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For instance, in the fraction 1/2, the denominator (2) tells us the whole is divided into two equal parts, and the numerator (1) tells us we are considering one of those parts. Similarly, in 1/8, the whole is divided into eight equal parts, and we are considering only one part.
Comparing 1/2 and 1/8: Visual Representation
One of the simplest ways to compare fractions is through visual representation. Imagine two identical pizzas.
Pizza 1: Representing 1/2
Cut the first pizza into two equal halves. Taking one of these halves represents the fraction 1/2.
Pizza 2: Representing 1/8
Cut the second pizza into eight equal slices. Taking one of these slices represents the fraction 1/8.
By visually comparing the size of one half of Pizza 1 to one slice of Pizza 2, it's immediately clear that 1/2 is significantly larger than 1/8. The visual representation provides an intuitive understanding of the relative sizes of these fractions.
Comparing Fractions Using Common Denominators
A more formal and mathematically rigorous approach involves finding a common denominator. A common denominator is a number that is a multiple of both denominators. In this case, the denominators are 2 and 8. The least common multiple (LCM) of 2 and 8 is 8.
Converting to a Common Denominator
To convert 1/2 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 4:
(1 × 4) / (2 × 4) = 4/8
Now we can easily compare 4/8 and 1/8. Since both fractions have the same denominator, we simply compare the numerators. Clearly, 4 is greater than 1. Therefore, 4/8 (which is equivalent to 1/2) is greater than 1/8.
Comparing Fractions Using Decimal Equivalents
Another method involves converting the fractions to their decimal equivalents. To do this, we perform the division indicated by the fraction:
Converting 1/2 to a Decimal
1 ÷ 2 = 0.5
Converting 1/8 to a Decimal
1 ÷ 8 = 0.125
Comparing the decimal equivalents, we see that 0.5 is greater than 0.125. This confirms that 1/2 is greater than 1/8.
Understanding the Relationship: Proportional Reasoning
The comparison of 1/2 and 1/8 highlights the importance of understanding proportional reasoning. As the denominator increases (meaning we're dividing the whole into more pieces), the size of each individual piece decreases. Therefore, 1/8 represents a smaller portion of the whole than 1/2.
Extending the Concept: Comparing Any Two Fractions
The methods discussed above – visual representation, common denominators, and decimal conversion – are applicable to comparing any two fractions. Choosing the most efficient method often depends on the specific fractions involved and your personal preference. For fractions with easily identifiable common denominators, the common denominator method is often the quickest. For fractions that are easily converted to decimals, the decimal conversion method may be more convenient. Visual representation is particularly useful for building intuitive understanding, especially when working with younger learners.
Real-World Applications: Why Understanding Fraction Comparison Matters
The ability to compare fractions isn't just a mathematical exercise; it has numerous practical applications in everyday life. Here are a few examples:
-
Cooking and Baking: Recipes often require precise measurements, and understanding fractions is crucial for accurate ingredient proportions. For instance, knowing whether 1/2 cup is more than 1/8 cup is essential for successful baking.
-
Measurements and Construction: Construction and engineering projects often involve precise measurements, and the ability to compare fractions is vital for accurate calculations and ensuring structural integrity.
-
Finance and Budgeting: Managing finances effectively often involves working with fractions and percentages, and the ability to compare fractions is essential for budgeting and making informed financial decisions.
-
Data Analysis: In various fields, data is often represented using fractions and proportions. Understanding fraction comparison is essential for interpreting data accurately and drawing meaningful conclusions.
Advanced Fraction Comparison Techniques
For more complex scenarios involving comparing multiple fractions or fractions with larger numbers, more advanced techniques may be necessary. These include:
-
Cross-Multiplication: This technique involves multiplying the numerator of one fraction by the denominator of the other and vice versa. The fraction with the larger product has the greater value. This is particularly helpful when finding common denominators is cumbersome.
-
Using a Calculator: For very large or complex fractions, a calculator can be a valuable tool to quickly determine decimal equivalents and facilitate comparisons.
Conclusion: Mastering Fraction Comparison
The question of whether 1/2 is greater than 1/8 is a stepping stone to understanding a much broader concept: the comparison of fractions. Mastering this skill is fundamental to a strong grasp of mathematical reasoning and has wide-ranging applications in various aspects of life. By utilizing the various methods discussed in this article – visual representation, common denominators, decimal conversion, cross-multiplication – you can confidently compare any two fractions and confidently solve problems involving fractional quantities. Remember that consistent practice and the application of these methods in different contexts will solidify your understanding and enhance your ability to work with fractions effectively.
Latest Posts
Latest Posts
-
Find The Greatest Common Factor Of 50 25 And 100
May 10, 2025
-
How Long After Bleaching Hair Can You Color It
May 10, 2025
-
Is Methane A Compound Or An Element
May 10, 2025
-
What Is The Long Division Symbol Called
May 10, 2025
-
Are Lays Cheddar And Sour Cream Gluten Free
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Greater Than 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.